
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Курсовая работа: Математические основы теории систем
Курсовая работа: Математические основы теории систем
Саратовский Государственный Технический Университет
Балаковский Институт Техники Технологии и Управления
Кафедра:
Специальность:
Курсовая работа
МОТС
Выполнил:
Принял:
Балаково 2009г.
I-часть
Задание1: По виду электрической схемы построить математическую модель объекта управления в пространстве состояния.
Задание2: По построенной модели составить структурную схему и сигнальный граф.
Задание3: Используя формулу Мейсона найти передаточную функцию объекта управления.
Задание4: По передаточной функции объекта управления определить временные и частотные характеристики. Построить их зависимость: АЧХ, ФЧХ.
Задание5: По полученным зависимостям определить прямые и косвенные оценки качества объекта управления.
II-часть.
Задание1: По заданной корреляционной функции Kx(t) определить спектральную плотность Sx(w) для белого шума, который подается на вход формирующего фильтра.
Задание2: По заданным статистическим характеристикам Se,Sv определить передаточную функцию формирующего фильтра y(р)
Задание3: Представить объект управления в виде
 V(t) X(t) Y(t)
V(t) X(t) Y(t)
и оценить качество полученной системы по переходной характеристике.
Задание4: Сделать вывод по работе.
I-часть
Данные
| R1 | R2 | R3 | R4 | L1 | L2 | C2 | I2 |
Ом |
Гн. |
10-6Ф |
? | ||||
| 328 | 395 | 118 | 215 | 24 | 24 | 19605 | |
L1 e(t) L2
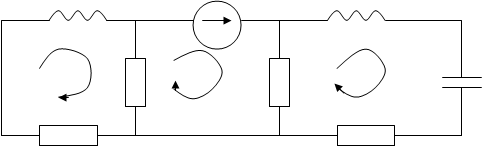
1. Построить математическую модель объекта управления в пространстве состояния.

В схеме три
элемента, запасающих энергию: ![]() ,
следовательно, математическая модель должна быть третьего порядка.
,
следовательно, математическая модель должна быть третьего порядка.
2. Построение математической модели.
Задаемся направлением
контурных токов ![]() . Составляем
три уравнения по второму закону Кирхгофа для контуров:
. Составляем
три уравнения по второму закону Кирхгофа для контуров:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
В уравнении (3) есть интеграл, поэтому дифференцируем его:
![]() (3*)
(3*)
В уравнениях
(3*), (2), (3) есть производные, в качестве ![]() выбираем элементы с производными и производные
берем на порядок ниже:
выбираем элементы с производными и производные
берем на порядок ниже:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Запишем введенный вектор состояния в виде дифференциальных уравнений первого порядка.
![]()
![]()
![]()
Уравнение в пространстве состояний записывается в левой части:
![]()
![]()
![]()
В полученных
уравнениях имеется шесть переменных ![]() . Необходимо уйти от
. Необходимо уйти от ![]() , выразив их через
, выразив их через ![]()
Из выражения (1)
выразим ![]() :
:
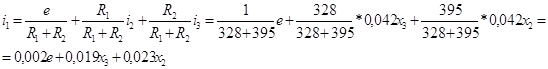
![]()
![]()
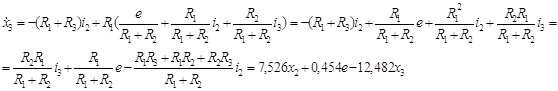
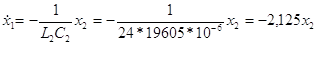
![]()
Получили три дифференциальных уравнения и одно уравнение для выходного параметра.
Запишем полученную систему уравнений в матричном виде:
![]()
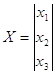
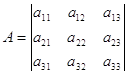
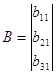
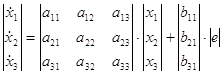
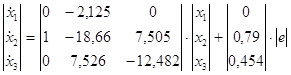
Получим матричное уравнение для выходной переменной:
![]()
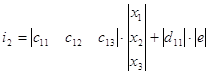
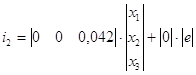
2. Построение сигнального графа.
Перепишем уравнения в общем, виде для построения графа системы:
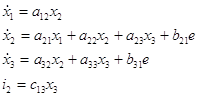
Построение графа произведем в два шага:
Шаг 1. Ставим
точки входа, выхода системы ![]() и
векторы параметров
и
векторы параметров
Шаг 2. Соединяем все параметры связями согласно системе уравнений.
|
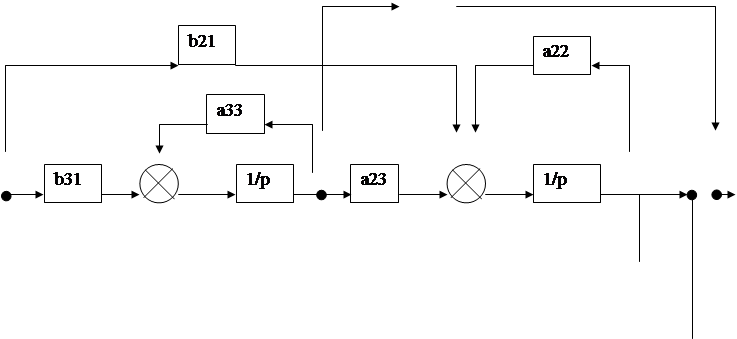
![]()
![]() e X 3
X 3 X 2 X 2 i2
e X 3
X 3 X 2 X 2 i2
|
|||||
X 1 X 1
3) Нахождение передаточной функции по формуле Мейсона.
k-количество возможных путей от входа к выходу
![]() -определитель
графа
-определитель
графа
Pk-коэффициент передачи k пути от входа к выходу
![]() -определитель всех касающихся контуров при
удалении k-ого пути
-определитель всех касающихся контуров при
удалении k-ого пути
![]() =1-(сумма коэффициентов передачи всех отдельных
контуров)+(сумма всевозможных произведений из двух некасающихся контуров) -
(сумма всевозможных комбинаций из трех некасающихся контуров)+…+…
=1-(сумма коэффициентов передачи всех отдельных
контуров)+(сумма всевозможных произведений из двух некасающихся контуров) -
(сумма всевозможных комбинаций из трех некасающихся контуров)+…+…
Последовательность нахождения w(p) по формуле Мейсона:
1) В данном случае есть 1 путь от входа к выходу:
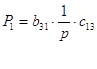
2) В системе имеется 4 замкнутых контуров:
![]()
![]()
![]()
![]()
3) Определитель системы включает 4 контура и 2 пары некасающихся контуров L1,L2; L1,L4
![]()
4)
Количество сомножителей равно количеству прямых путей. Выражение для ![]() записывается как выражение для
записывается как выражение для ![]() , но разрываются контуры, через
которые проходит прямой путь Pi.
, но разрываются контуры, через
которые проходит прямой путь Pi.
Сомножитель ![]() для
первого пути. При размыкании первого пути 2 контура размыкаются, кроме L2,L4
для
первого пути. При размыкании первого пути 2 контура размыкаются, кроме L2,L4
![]()
5) Запишем и преобразуем выражение передаточной функции:
![]()
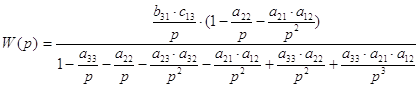
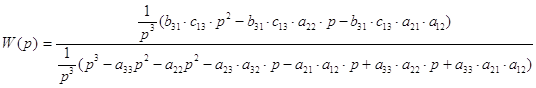
![]()
![]()
![]()
![]()
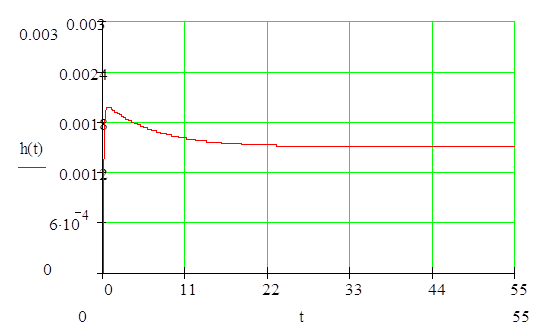
Найдем переходную функцию и построим ее график:
 |
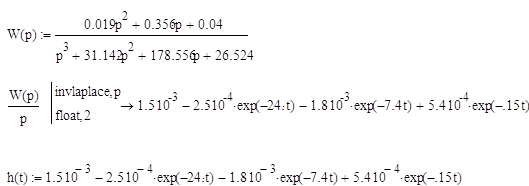 |
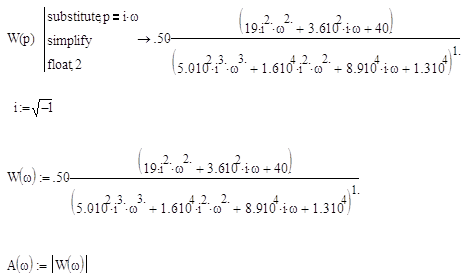 |
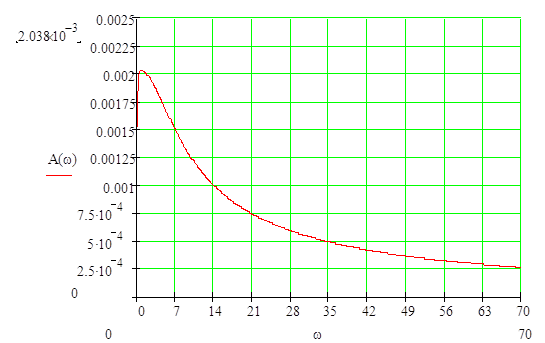
Найдем амплитудно-частотную характеристику (АЧХ):
 |
Найдем фаза частотную характеристику (ФЧХ):
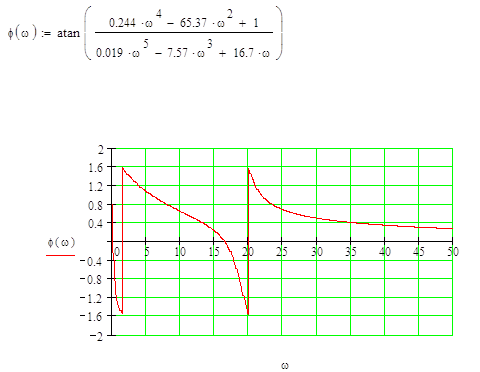 |
Определим оценки качества системы: прямые и косвенные.
Прямые оценки определяются графически по графику переходного процесса.
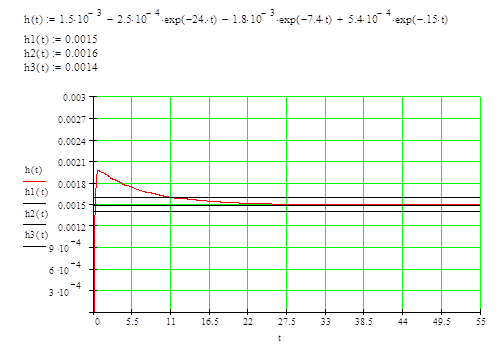 |
Время переходного процесса: tn=11
Перерегулирование:
![]()
Колебательность: п=0,5
Время нарастания регулируемой величины: t=0,385
Время первого согласования: tm=0,66
Косвенные оценки качества системы определяются по графику АЧХ.
Колебательность:
![]()
Резонансная частота: wp=0,83
Частота среза: wсp=10
![]()
Полоса
пропускания частот: ![]()
II-часть
Задание1: По заданной корреляционной функции Kx(t) определить спектральную плотность Sx(w) для белого шума, который подается на вход формирующего фильтра.
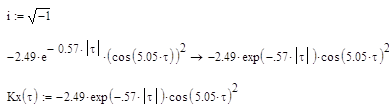 |
По данной корреляционной функции определим спектральную плотность:
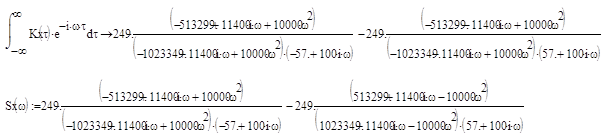 |
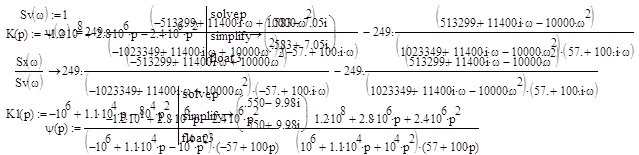 |
Найдем корни характеристических уравнений передаточной функции фильтра:
Изобразим эти корни на комплекснрй плоскости:
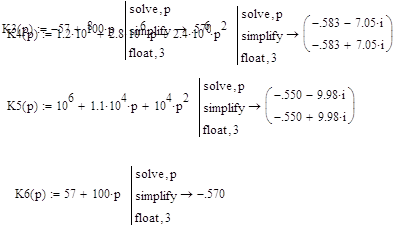 |
Система будет устойчивой, если корни характеристического уравнения лежат во 2-ом квадранте, следовательно, условию устойчивости системы соответствуют корни:
P7= -0,583+7,05i
P9= - 0,550+9,98i
P10= -0,570
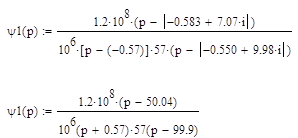 |
Из этого следует, что передаточная функция фильтра будет иметь
следующий вид:
С учетом фильтра наша схема будет иметь следующий вид:
![]()
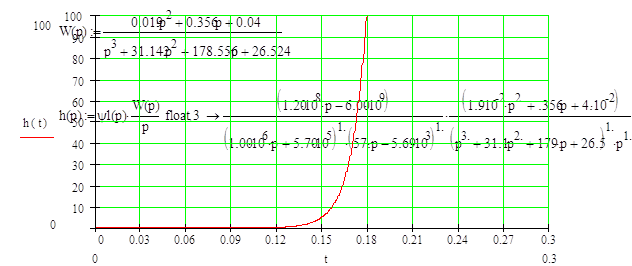
Найдем переходную функцию данной системы, построим ее график и определим прямые
оценки качества системы.
Вывод: По графику видно, что фильтр вносит в систему изменения, приводящие к неустойчивости системы. Вследствие чего оценки качества системы определить нельзя.