
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Курсовая работа: Создание макроса на языке Statistica Visual Basic для проверки гипотезы о нормальности остатков регрессии
Курсовая работа: Создание макроса на языке Statistica Visual Basic для проверки гипотезы о нормальности остатков регрессии
СОДЕРЖАНИЕ
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ И ТЕРМИНОВ
ВВЕДЕНИЕ
1. ПРОГРАММИРОВАНИЕ В STATISTICA
2. ПРЕДПОСЫЛКИ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ И ИХ РЕАЛИЗАЦИЯ В STATISTICA
2.1. Модель множественной линейной регрессии
2.2. Требования к остаткам
2.3. Проверка гипотезы о нормальности остатков в модуле MULTIPLE REGRESSION STATISTICA
3. СОЗДАНИЕ МАКРОСА ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О НОРМАЛЬНОСТИ ОСТАТКОВ
3.1. Описание макроса
3.2. Проверка гипотезы о нормальности остатков в модели вторичного рынка жилья в г. Минске
ЗАКЛЮЧЕНИЕ
ПРИЛОЖЕНИЕ А. Листинг программы
ПРИЛОЖЕНИЕ Б. Листинг программы
ПРИЛОЖЕНИЕ В. Глобальные переменные
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ И ТЕРМИНОВ
SVB - Statistica Visual Basic.
МНК - метод наименьших квадратов.
ВВЕДЕНИЕ
Множественная линейная регрессия выражает линейные связи между переменными в уравнении при нормальном распределении остатков. Если эти предположения нарушены, заключение не может быть точным, т.е. модель не может быть использована для принятия решений и осуществления прогнозов. В связи с этим при построении модели множественной линейной регрессии особое внимание необходимо уделять проверке гипотезы о нормальном распределении остатков.
Создание макросов - полезная и зачастую необходимая процедура, которая присутствует во многих программных продуктах, в том числе и в программе STATISTICA. Основное ее назначение - автоматизация обработки данных и соответственно значительная экономия времени. В ходе выполнения множественного регрессионного анализа в модуле Multiple Regression пакета STATISTICA исследование остатков на нормальность можно осуществить лишь графическими методами, что приводит к необходимости обращаться к другому встроенному модулю (Distribution Fitting), что требует значительных затрат времени. Для решения данной проблемы был написан макрос на языке SVB.
Предметом исследования данной работы является создание макроса для проверки гипотезы о нормальности остатков множественной регрессии.
Целью данной курсовой работы является создание макроса на языке SVB для проверки гипотезы о нормальности остатков множественной регрессии.
Для достижения поставленной цели необходимо решить следующие задачи:
- изучить возможности программирования на языке SVB в пакете STATISTICA;
- рассмотреть модель множественной линейной регрессии и предпосылки МНК;
- описать процесс проверки гипотезы о нормальности остатков в модуле MULTIPLE REGRESSION STATISTICA;
- создать макрос для проверки гипотезы о нормальности остатков;
- осуществить проверку гипотезы о нормальности остатков в модели вторичного рынка жилья в г. Минске.
В курсовой работе использованы анализ и синтез, аналитический метод, графический метод, методы моделирования и проектирования.
Работа представлена на 48 страницах и состоит из введения, трех разделов (пяти подразделов), заключения, списка использованных источников, приложений.
В первом разделе исследуются возможности программирования на языке SVB в пакете STATISTICA. Во втором разделе раскрываются предпосылки МНК и их реализация в STATISTICA. Третий раздел носит исследовательский характер. В нем описывается создание и применение макроса для проверки гипотезы о нормальности остатков.
В данной курсовой работе была использована литература отечественных и зарубежных авторов. Большое внимание уделялось учебным пособиям таких авторов, как И.И. Елисеева, О.Н. Салманов, Кристофер Доугерти и др. При написании курсовой работы также были использованы данные Интернет-источников.
1. ПРОГРАММИРОВАНИЕ В STATISTICA
STATISTICA Visual Basic (SVB) - это язык программирования, интегрированный в программу STATISTICA. Он предоставляет намного больше возможностей, чем просто "вспомогательный язык программирования". SVB использует огромные преимущества объектно-ориентированной структуры системы STATISTICA и позволяет получить доступ практически ко всем функциональным возможностям пакета программными средствами. [советник по макросам-СПМ]
Очень часто при статистической обработке однотипных наборов данных приходится периодически и многократно выполнять одну и ту же серию операций. Сложные процедуры анализа и графический вывод результатов можно записать как макрос SVB для дальнейшего использования и редактирования. Макросы представляют собой самостоятельные блоки, которые легко встраиваются в другие приложения. [советник по макросам-СПМ]
Существует несколько методов создания макросов SVB:
1. Автоматическая запись макроса. Каждый раз при выполнении процедур из меню Statistics или Graphs, SVB записывает в фоновом режиме программный код, соответствующий всем спецификациям процедур и параметрам вывода. Этот код может впоследствии многократно выполняться и редактироваться. В процессе редактирования можно изменять настройки процедур анализа, используемые переменные и их спецификации, файлы данных, добавлять элементы пользовательского интерфейса и т.д.
2. Макросы могут быть написаны с нуля с помощью профессиональной среды разработчика SVB (рис.1). Данная среда представляет собой удобный редактор программного кода с мощным отладчиком. Кроме того, имеется наглядный мастер создания диалогов, а также множество других удобных функций для эффективного написания макросов.
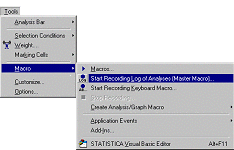
Рис. 1. Диалог Macros
3. SVB макросы могут создаваться на основе уже готовых программ на VISUAL BASIC, написанных в других приложениях (например, MICROSOFT EXCEL), путем добавления встроенных процедур и функций STATISTICA.[scaner 497-498]
В STATISTICA предусмотрено три категории макросов, которые могут быть автоматически написаны. Для активации этих макросов в меню Tools на панели инструментов выделите команду Macro (рис.2). [scaner c. 498]
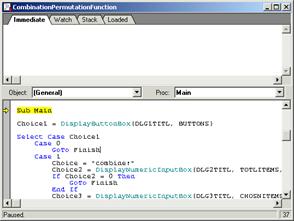
Рис. 2. Редактор макросов VISUAL BASIC
1. Analysis/Graph Macro (макрос анализа/графика) - макросы, создаваемые для конкретных типов анализа из меню Statistics и Graphs. В макрос записываются все настройки, параметры, присущие данному типу анализа, а также переменные, над которыми он проводится. После выбора модуля или процедуры из указанных меню в фоновом режиме осуществляется запись всех выполняемых действий: выбор переменных, изменение параметров и др. В любой момент можно перенести записанную информацию (код макроса VISUAL BASIC) в окно редактора макросов VISUAL BASIC (см. рис. 1).
2. Log of Analyses (Master Macro) (мастер-макрос (журнал)) - макросы, содержащие любую последовательность модулей из меню Statistics или Graphs. В мастер-макрос записывается последовательность проведенных анализов с указанными для них параметрами и переменными от момента включения записи макроса до ее отключения. Такая запись объединяет различные модули, выбранные в меню Statistics или Graphs. В отличие от простого Analysis Macro, запись Master Macros может быть приостановлена и возобновлена. Запись мастера-макроса начинается при нажатии кнопки записи и приостанавливается нажатием кнопки останова. Все действия, совершенные между этими событиями, записываются в соответствующей последовательности: выбор файлов данных, операции преобразования переменных, выбор элементов и др.
3. Key board Macro (клавиатурный макрос) - макросы, содержащие последовательности нажатия клавиш во время проведения анализа. При остановке записи в окне редактора SVB откроется простая программа, содержащая одну команду SendKeys с символами, которые соответствуют клавишам, нажатым при проведении анализа. Данный тип макроса довольно прост - он не записывает контекст, в котором происходило нажатие клавиш (т.е. команды, которые при этом выбирались), но данное свойство может быть полезно для решения определенных задач.
Все три категории макросов имеют одинаковый синтаксис и могут быть впоследствии модифицированы. [scaner c.499]
Среда разработки STATISTICA Visual Basic (см. рис. 2) содержит гибкий редактор программ и мощные средства отладки.
Отладка макросов. Среда разработки SVB позволяет устанавливать в программе точки останова, если необходимо приостановить работу макроса на какой-либо строке и проверить значение переменных в этой точке программы. Предусмотрена возможность выполнения макроса по шагам.
Диспетчер объектов. Объекты в SVB организованы в виде иерархического дерева объектов, и этот список можно найти в окне Object Browser - Просмотр объектов (рис. 3).
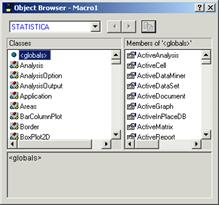
Рис.3. Окно Object Browser - Просмотр объектов.
Мастер функций. Существует множество функций STATISTICA и как правило, они доступны только в SVB. Это расширение языка программирования Visual Basic, например, вероятностные, матричные функции, простые окна диалогов пользователя и т.д.
Редактор диалогов пользователя. Среда программирования SVB содержит все необходимые средства для создания пользовательского интерфейса. Мощные средства User-Dialog Editor - Редактора диалогов позволяют проектировать диалоговые окна, используя мышь. В отличие от Microsoft Visual Basic, созданные пользователем диалоги хранятся вместе с программным кодом как данные типа UserDialog. Такой метод создания диалоговых окон позволяет реализовывать сложные элементы интерфейса, которые легко редактируются в текстовом режиме; кроме того, определяя диалог, как переменную, к нему легко можно обращаться в любом месте программы.
2. ПРЕДПОСЫЛКИ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ И ИХ РЕАЛИЗАЦИЯ В STATISTICA
2.1 Модель множественной линейной регрессии
В экономической практике часто имеет место сложная, многопричинная статистическая связь между признаками.
Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т.е. модель вида:
![]() [Елисеева-34]
[Елисеева-34]
Переменная ![]() называется зависимой переменной, в
то время как переменные
называется зависимой переменной, в
то время как переменные ![]() называются
независимыми переменными.[Afifi-164]
называются
независимыми переменными.[Afifi-164]
Задача оценки
статистической взаимосвязи переменных ![]() и
и ![]() формулируется аналогично
случаю парной регрессии. Записывается функция
формулируется аналогично
случаю парной регрессии. Записывается функция ![]() ,
где b- вектор параметров,
,
где b- вектор параметров, ![]() -случайная ошибка.
Предполагается, что эта функция связывает переменную
-случайная ошибка.
Предполагается, что эта функция связывает переменную ![]() с вектором независимых переменных
с вектором независимых переменных ![]() для данной генеральной совокупности. Предполагается,
что ошибки
для данной генеральной совокупности. Предполагается,
что ошибки ![]() являются случайными
величинами с нулевым математическим ожиданием и постоянной дисперсией;
являются случайными
величинами с нулевым математическим ожиданием и постоянной дисперсией; ![]() и
и ![]() статистически
независимы при
статистически
независимы при ![]() . Кроме
того, для проверки статистической значимости оценок b обычно предполагается, что ошибки
. Кроме
того, для проверки статистической значимости оценок b обычно предполагается, что ошибки ![]() нормально распределены.
нормально распределены.
Для оценивания параметров
![]() применяется, как правило,
метод наименьших квадратов. Уравнение регрессии с оцененными параметрами имеет вид
применяется, как правило,
метод наименьших квадратов. Уравнение регрессии с оцененными параметрами имеет вид
![]() .[Салманов-44]
.[Салманов-44]
Практически в каждом отдельном случае величина у складывается из двух слагаемых:
![]()
где ![]() -фактическое значение результативного признака;
-фактическое значение результативного признака;
![]() -теоретическое значение результативного признака, найденное
исходя из соответствующей математической функции связи
-теоретическое значение результативного признака, найденное
исходя из соответствующей математической функции связи ![]() и
и ![]() , т. е. из
уравнения регрессии;
, т. е. из
уравнения регрессии;
![]() - случайная величина, характеризующая отклонения
реального значения результативного признака от теоретического, найденного по
уравнению регрессии. . [Елисеева-35]
- случайная величина, характеризующая отклонения
реального значения результативного признака от теоретического, найденного по
уравнению регрессии. . [Елисеева-35]
Общий смысл оценивания по
методу наименьших квадратов заключается в минимизации суммы квадратов
отклонений наблюдаемых значений зависимой переменной (![]() ) от значений,
предсказанных моделью(
) от значений,
предсказанных моделью(![]() ).
).
![]() ,
,
где S- суммы квадратов отклонений
![]() -остаток в наблюдении j.[net]
-остаток в наблюдении j.[net]
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Она включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. [Елисеева-91]
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. [Елисеева-92] Для исследования влияния качественных признаков в модель можно вводить бинарные (фиктивные) переменные, которые, как правило, принимают значение 1, если данный качественный признак присутствует в наблюдении, и значение 0 при его отсутствии.[Магнус 100]
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. [Елисеева-92]
Коэффициенты
интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют
исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны,
т. е. находятся между собой в линейной зависимости, если ![]() .
.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК). [Елисеева-94]
Выделим некоторые наиболее характерные признаки мультиколлинеарности.
1. Небольшое изменение исходных данных (например, добавление новых наблюдений) приводит к существенному изменению оценок коэффициентов модели.
2. Оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой (высокое значение коэффициента детерминации R2 и соответствующей F-статистики).
3. Оценки коэффициентов имеют неправильные с точки зрения теории знаки или неоправданно большие значения.[Магнус 94]
Подходы к отбору факторов на основе показателей корреляции могут быть разные. Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
• метод исключения;
• метод включения;
• шаговый регрессионный анализ.
Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты - отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).
Как и в парной
зависимости, возможны разные виды уравнений множественной регрессии: линейные и
нелинейные. [Елисеева-100] Линейные модели регрессии могут быть описаны как
линейные в двух отношениях: как линейные по переменным и как линейные по
параметрам. Для линейного регрессионного анализа требуется линейность только по
параметрам (![]() ),
поскольку нелинейность по переменным (
),
поскольку нелинейность по переменным (![]() )
может быть устранена с помощью изменения определений.[Доугерти 141]
)
может быть устранена с помощью изменения определений.[Доугерти 141]
В линейной множественной
регрессии параметры при х называются коэффициентами регрессии (![]() ). Они характеризуют
среднее изменение результата (
). Они характеризуют
среднее изменение результата (![]() )
с изменением соответствующего фактора (
)
с изменением соответствующего фактора (![]() )
на единицу при неизмененном значении других факторов, закрепленных на среднем
уровне. [Елисеева-100]
)
на единицу при неизмененном значении других факторов, закрепленных на среднем
уровне. [Елисеева-100]
Оценка значимости коэффициентов чистой регрессии может быть проведена по t-критерию Стьюдента. В этом случае, как и в парной регрессии, для каждого фактора используется формула:
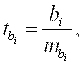
где ![]() - коэффициент чистой
регрессии при факторе хi;
- коэффициент чистой
регрессии при факторе хi;
![]() - средняя квадратическая ошибка
коэффициента регрессии
- средняя квадратическая ошибка
коэффициента регрессии ![]() .
.
Для уравнения
множественной регрессии ![]()
средняя квадратическая
ошибка коэффициента регрессии ![]() может быть определена по следующей формуле:
может быть определена по следующей формуле:

где ![]() - среднее квадратическое
отклонение для признака у;
- среднее квадратическое
отклонение для признака у;
![]() - среднее квадратическое отклонение
для признака
- среднее квадратическое отклонение
для признака ![]() ;
;
![]() - коэффициент детерминации для
уравнения множественной регрессии;
- коэффициент детерминации для
уравнения множественной регрессии;
![]() - коэффициент детерминации для
зависимости фактора
- коэффициент детерминации для
зависимости фактора ![]() со
всеми другими факторами уравнения множественной регрессии;
со
всеми другими факторами уравнения множественной регрессии;
![]() - число степеней свободы для остаточной
суммы квадратов отклонений. [Елисеева-136-137]
- число степеней свободы для остаточной
суммы квадратов отклонений. [Елисеева-136-137]
Критический уровень t при любом уровне значимости зависит
от числа степеней свободы, которое равно ![]() : число наблюдений минус число
оцененных параметров. [Доугерти 154]
: число наблюдений минус число
оцененных параметров. [Доугерти 154]
Практическая значимость
уравнения множественной регрессии оценивается с помощью показателя
множественной корреляции (![]() ) и его
квадрата – коэффициента детерминации (
) и его
квадрата – коэффициента детерминации (![]() ).
[Елисеева-112]
).
[Елисеева-112]
Показатель множественной корреляции может быть найден как индекс множественной корреляции:

где ![]() - общая дисперсия
результативного признака;
- общая дисперсия
результативного признака;
![]() - остаточная дисперсия для уравнения
- остаточная дисперсия для уравнения
![]()
Границы изменения индекса множественной корреляции: от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. [Елисеева-113]
Коэффициент детерминации ![]() определяет долю дисперсии
определяет долю дисперсии ![]() , объясненную
регрессией. [Доугерти 159]
, объясненную
регрессией. [Доугерти 159]
Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:
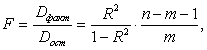
где ![]() - факторная сумма квадратов на одну степень свободы;
- факторная сумма квадратов на одну степень свободы;
![]() - остаточная сумма квадратов на одну степень свободы;
- остаточная сумма квадратов на одну степень свободы;
![]() - коэффициент (индекс) множественной
детерминации;
- коэффициент (индекс) множественной
детерминации;
![]() - число параметров при переменных
- число параметров при переменных ![]() (в линейной
регрессии совпадает с числом включенных в модель факторов);
(в линейной
регрессии совпадает с числом включенных в модель факторов);
![]() - число наблюдений. [Елисеева-129]
- число наблюдений. [Елисеева-129]
Смысл проверяемой гипотезы заключается в том, что все коэффициенты линейной регрессии, за исключением свободного параметра, равны нулю (случай отсутствия линейной функциональной связи).
![]()
Величина F имеет
распределение Фишера с степенями свободы ![]() . Распределение Фишера -
двухпараметрическое распределение неотрицательной случайной величины,
являющейся в частном случае при m = 1
квадратом случайной величины, распределенной по Стьюденту. [Салманов 48]. В
определенном смысле этот тест дополняет t-тесты, которые используются для проверки значимости вклада
отдельных случайных переменных, когда проверяется каждая из гипотез
. Распределение Фишера -
двухпараметрическое распределение неотрицательной случайной величины,
являющейся в частном случае при m = 1
квадратом случайной величины, распределенной по Стьюденту. [Салманов 48]. В
определенном смысле этот тест дополняет t-тесты, которые используются для проверки значимости вклада
отдельных случайных переменных, когда проверяется каждая из гипотез ![]() .. [Доугерти 160]
.. [Доугерти 160]
Для проверки нулевой
гипотезы при заданном уровне значимости по таблицам находится критическое
значение Fкрит, и нулевая гипотеза отвергается, если ![]() .
.
Распределение Фишера может быть использовано не только для проверки гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии, но и гипотезы о равенстве нулю части этих коэффициентов. Это особенно важно при развитии линейной регрессионной модели, так как позволяет оценить обоснованность исключения отдельных переменных или их групп из числа объясняющих переменных или, наоборот, включения их в это число. [Салманов 48].
2.2 Требования к остаткам
При оценке параметров
уравнения регрессии применяется метод наименьших квадратов (МНК). При этом
делаются определенные предпосылки относительно случайной составляющей ![]() . В модели
. В модели
![]()
случайная составляющая ![]() представляет собой ненаблюдаемую
величину. В задачу регрессионного анализа входит не только построение самой
модели, но и исследование случайных отклонений
представляет собой ненаблюдаемую
величину. В задачу регрессионного анализа входит не только построение самой
модели, но и исследование случайных отклонений ![]() , т. е. остаточных величин.
, т. е. остаточных величин.
Проверка статистической
достоверности коэффициентов регрессии и корреляции осуществляется с помощью t-критерия Стьюдента, F-критерия Фишера и Z-преобразования (для коэффициентов
корреляции). При использовании этих критериев делаются предположения
относительно поведения остатков ![]() - остатки представляют собой независимые случайные
величины и их среднее значение равно 0; они имеют одинаковую (постоянную)
дисперсию и подчиняются нормальному распределению.
- остатки представляют собой независимые случайные
величины и их среднее значение равно 0; они имеют одинаковую (постоянную)
дисперсию и подчиняются нормальному распределению.
Оценки параметров регрессии должны быть несмещенными, состоятельными и эффективными. Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.
Исследования остатков ![]() предполагают проверку наличия
следующих пяти предпосылок МНК:
предполагают проверку наличия
следующих пяти предпосылок МНК:
1) случайный характер остатков;
2) нулевая средняя величина остатков, не
зависящая от ![]() ;
;
3) гомоскедастичность - дисперсия каждого отклонения ![]() одинакова для всех значений х;
одинакова для всех значений х;
4) отсутствие автокорреляции остатков.
Значения остатков ![]() распределены независимо друг от друга;
распределены независимо друг от друга;
5) остатки подчиняются нормальному распределению.
Если распределение
случайных остатков ![]() не соответствует некоторым предпосылкам МНК, то
следует корректировать модель.
не соответствует некоторым предпосылкам МНК, то
следует корректировать модель.
Прежде всего проверяется
случайный xapактер остатков ![]() - первая предпосылка МНК.
- первая предпосылка МНК.
С этой целью стоится
график зависимости остатков ![]() от теоретических значений результативного признака
(рис. 3.2).
от теоретических значений результативного признака
(рис. 3.2).
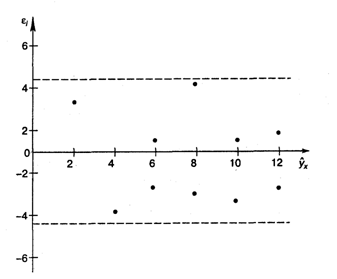
Рис.3.2. Зависимость
случайных остатков ![]() от теоретических значений
от теоретических значений ![]()
Если на графике получена
горизонтальная полоса, то остатки ![]() представляют собой случайные величины и MНK оправдан, теоретические значения
представляют собой случайные величины и MНK оправдан, теоретические значения ![]() хорошо аппроксимирует
фактические значения у.
хорошо аппроксимирует
фактические значения у.
Возможны следующие
случаи: если ![]() зависит от
зависит от ![]() , то:
, то:
а) остатки ![]() не случайны;
не случайны;
б) остатки ![]() не имеют постоянной дисперсии;
не имеют постоянной дисперсии;
в) остатки ![]() носят систематический характер.
носят систематический характер.
В случаях а), б), в)
необходимо либо применять другую функцию, либо вводить дополнительную
информацию и заново строить уравнение регрессии до тех пор, пока остатки ![]() не будут случайными величинами.
не будут случайными величинами.
Вторая предпосылка МНК
относительно нулевой средней величины остатков означает, что![]() . Это выполнимо для линейных моделей
и моделей, нелинейных относительно включаемых переменных.
. Это выполнимо для линейных моделей
и моделей, нелинейных относительно включаемых переменных.
Вместе с тем
несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от
независимости случайных остатков и величин х, что также исследуется в
рамках соблюдения второй предпосылки МНК. С этой целью строится график
зависимости случайных остатков ![]() от факторов, включенных в регрессию
от факторов, включенных в регрессию ![]() (рис. 3.4).
(рис. 3.4).
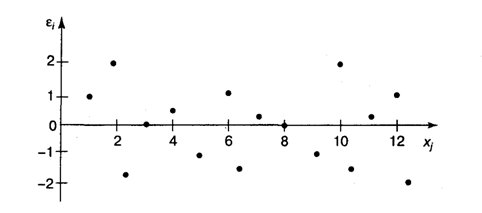
Рис. 3.4. Зависимость
случайных остатков от величины фактора ![]()
Если остатки на графике
расположены в виде горизонтальной полосы (рис. 3.4), то они независимы от
значений ![]() . Если же график показывает наличие зависимости
. Если же график показывает наличие зависимости ![]() и
и ![]() , то модель неадекватна.
, то модель неадекватна.
Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t, F.[1] Всегда, прежде чем сделать окончательные выводы, стоит рассмотреть распределения представляющих интерес переменных. Можно построить гистограммы или нормальные вероятностные графики остатков для визуального анализа их распределения.[электрон-уч]
В соответствии с третьей
предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной.
Это значит, что для каждого значения фактора ![]() остатки
остатки ![]() имеют одинаковую дисперсию. Если это условие
применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие
гетероскедастичности можно наглядно видеть из поля корреляции (рис. 3.5).
имеют одинаковую дисперсию. Если это условие
применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие
гетероскедастичности можно наглядно видеть из поля корреляции (рис. 3.5).
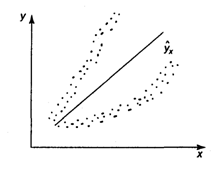
Рис. 3.5. Пример гетероскедастичности: дисперсия остатков растет по мере увеличения х;
Используя трехмерное изображение, получим следующие графики, иллюстрирующие гомо- и гетероскедастичность (рис. 3.6, 3.7).
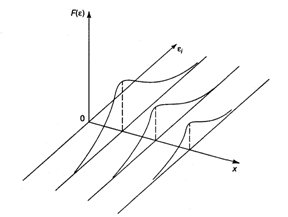
Рис. 3.6. Гомоскедастичность остатков

Рис. 3.7. Гетероскедастичность остатков
Рис. 3.6 показывает, что
для каждого значения ![]() распределения остатков
распределения остатков ![]() одинаковы в отличие от рис. 3.7, где диапазон варьирования остатков
меняется с переходом от одного значения
одинаковы в отличие от рис. 3.7, где диапазон варьирования остатков
меняется с переходом от одного значения ![]() другому. Соответственно на рис. 3.7 демонстрируется неодинаковая
дисперсия при разных значениях
другому. Соответственно на рис. 3.7 демонстрируется неодинаковая
дисперсия при разных значениях ![]() .
.
Наличие
гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному
выше графику зависимости остатков ![]() от теоретических значений результативного признака
от теоретических значений результативного признака ![]() . Так, для рис 3.5 зависимость
остатков от
. Так, для рис 3.5 зависимость
остатков от ![]() представлена
на рис. 3.8.
представлена
на рис. 3.8.
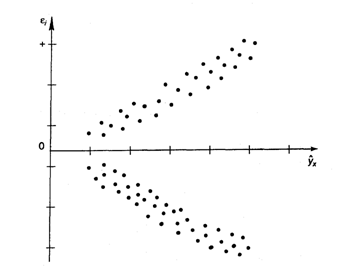
Рис. 3.8. Гетероскедастичность: большая
дисперсия ![]() для больших значений
для больших значений ![]()
При построении
рефессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК -
отсутствие автокорреляции остатков, т. е. значения остатков ![]() , распределены независимо друг от
друга. Автокорреляция остатков означает наличие корреляции между
остатками текущих и предыдущих (последующих) наблюдений. [1]
, распределены независимо друг от
друга. Автокорреляция остатков означает наличие корреляции между
остатками текущих и предыдущих (последующих) наблюдений. [1]
Одним из основных
предполагаемых свойств отклонений ![]() от регрессионной модели является их статистическая
независимость между собой. Поскольку значени
от регрессионной модели является их статистическая
независимость между собой. Поскольку значени ![]() остаются неизвестными, то проверяется статистическая независимость их
аналогов — отклонения
остаются неизвестными, то проверяется статистическая независимость их
аналогов — отклонения ![]() (наблюдаемые значения ошибок). При этом устанавливается
некоррелированность сдвинутыми на период величинами
(наблюдаемые значения ошибок). При этом устанавливается
некоррелированность сдвинутыми на период величинами ![]() . Для этих величин можно рассчитать
коэффициент автокорреляции первого порядка (выборочный коэффициент корреляции
между
. Для этих величин можно рассчитать
коэффициент автокорреляции первого порядка (выборочный коэффициент корреляции
между ![]() и
и ![]() ):
):
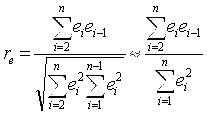
На практике в качестве
теста используют тесно связанную с коэффициентом автокорреляции ![]() статистику Дарбина — Уотсона. Тест Дарбина
Уотсона (DW) на наличие или отсутствие
автокорреляции ошибок рассчитывается по формуле:
статистику Дарбина — Уотсона. Тест Дарбина
Уотсона (DW) на наличие или отсутствие
автокорреляции ошибок рассчитывается по формуле:

Нулевая гипотеза состоит в отсутствии автокорреляции. Статистику Дарбина-Уотсона можно выразить через коэффициент автокорреляции:
![]() [2]
[2]
Содержательный смысл
статистики Дарбина-Уотсона заключается в следующем: если между ![]() и
и ![]() имеется достаточно высокая
положительная корреляция, то
имеется достаточно высокая
положительная корреляция, то ![]() и
и
![]() близки друг другу и
величина статистики DW мала.
Это согласуется с
последним выражением: если коэффициент
близки друг другу и
величина статистики DW мала.
Это согласуется с
последним выражением: если коэффициент ![]() близок
к единице, то величина DW
близка к нулю. Отсутствие корреляции означает, что DW близка к 2. [3]
близок
к единице, то величина DW
близка к нулю. Отсутствие корреляции означает, что DW близка к 2. [3]
Если бы распределение
статистики DW было известно, то для проверки
гипотезы ![]() против альтернативы
против альтернативы ![]() можно было бы для заданного
уровня значимости (например, для 5%-уровня) найти такое критическое значение
можно было бы для заданного
уровня значимости (например, для 5%-уровня) найти такое критическое значение ![]() , что если
, что если![]() , то гипотеза Но
не отвергается, в противном случае она отвергается в пользу Н1.
Проблема, однако, состоит в том, что распределение DW зависит не только от числа наблюдений п и
количества регрессоров к, но и от всей матрицы X, и, значит, практическое применение этой процедуры
невозможно. Тем не менее, Дарбин и Уотсон доказали, что существуют две границы,
обычно обозначаемые
, то гипотеза Но
не отвергается, в противном случае она отвергается в пользу Н1.
Проблема, однако, состоит в том, что распределение DW зависит не только от числа наблюдений п и
количества регрессоров к, но и от всей матрицы X, и, значит, практическое применение этой процедуры
невозможно. Тем не менее, Дарбин и Уотсон доказали, что существуют две границы,
обычно обозначаемые ![]() и
и ![]() ,
, ![]() (и = upper - верхняя, l = low - нижняя), которые зависят лишь от n, к и уровня значимости (а
следовательно, могут быть затабулированы) и обладают следующим свойством: если
(и = upper - верхняя, l = low - нижняя), которые зависят лишь от n, к и уровня значимости (а
следовательно, могут быть затабулированы) и обладают следующим свойством: если![]() , то
, то ![]() и, значит, гипотеза
H0 не отвергается, а если
и, значит, гипотеза
H0 не отвергается, а если ![]() то
то![]() , и гипотеза Но
отвергается в пользу H1. В
случае
, и гипотеза Но
отвергается в пользу H1. В
случае ![]() ситуация неопределенна, т.
е. нельзя высказаться в пользу той или иной гипотезы. Если альтернативной
является гипотеза об отрицательной корреляции
ситуация неопределенна, т.
е. нельзя высказаться в пользу той или иной гипотезы. Если альтернативной
является гипотеза об отрицательной корреляции![]() ,
то соответствующими верхними и нижними границами будут 4-dl и 4-du. Целесообразно представить эти результаты в виде
следующей таблицы.
,
то соответствующими верхними и нижними границами будут 4-dl и 4-du. Целесообразно представить эти результаты в виде
следующей таблицы.
Таблица 6.3.
Значение статистики DW
| Значение статистики DW | Вывод |
| 4 -dl< DW < 4 | Гипотеза Но отвергается, есть отрицательная корреляция |
| 4 - du < DW < 4 - dl | Неопределенность |
| du < DW < 4 - du | Гипотеза Но не отвергается |
| dl < DW < du | Неопределенность |
| 0 < DW < dl | Гипотеза Но отвергается, есть положительная корреляция |
Наличие зоны неопределенности, представляет определенные трудности при использовании теста Дарбина-Уотсона. [3]
Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять (исключать) некоторые факторы, преобразовывать исходные данные для того, чтобы получить оценки коэффициентов регрессии, которые обладают свойством несмещенности, имеют меньшее значение дисперсии остатков и обеспечивают в связи с этим более эффективную статистическую проверку значимости параметров регрессии. [1]
2.3 Проверка гипотезы о нормальности остатков в модуле Multiple Regression Statistica
STATISTICA является интегрированной системой комплексного статистического анализа и обработки данных в среде Windows. Все методы обработки в системе разбиты на несколько групп - модулей - в соответствии с основными разделами статистического анализа. Модуль Multiple Regression -Множественная регрессия включает в себя набор средств множественной линейной и фиксированной нелинейной (в частности, полиномиальной, экспоненциальной, логарифмической и др.) регрессии, включая пошаговые, иерархические и другие методы. Система STATISTICA позволяет вычислить всесторонний набор статистик и расширенной диагностики, включая полную регрессионную таблицу, частные и частичные корреляции и ковариации для регрессионных весов, статистику Дарбина-Уотсона и многие другие. Анализ остатков и выбросов может быть проведен при помощи широкого набора графиков. [Салманов, с. 245-246]
Модуль Multiple Regression запускается из меню Statistics. Нажмите кнопку Variable на Multiple Linear Regression - Quick tab (Множественная линейная регрессия - Быстрая вкладка) (рис. 1) и выберите зависимую переменную (Dependent variable) и несколько независимых переменных (Independent variable) и затем нажмите кнопку ОК. Появится Multiple Regression Results - диалог результатов регрессионного анализа (рис. 2). [Салманов, с. 249]
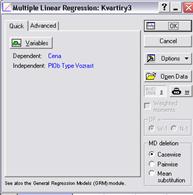
Рис. 1. Стартовая панель модуля Multiple Regression
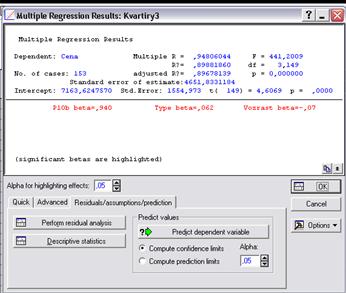
Рис. 2. Окно результатов регрессионного анализа
Окно результатов анализа (Multiple Regression Results) (рис. 2) имеет следующую структуру: верх окна - информационный. Он состоит из двух частей: в первой части содержится основная информация о результатах оценивания, во второй высвечиваются значимые регрессионные коэффициенты (significant beta's are highlighted). Внизу окна расположены три вкладки: Quick-быстрый, Advanced-продвинутый и Residuals/assumptions/ prediction, на которых находятся функциональные кнопки, позволяющие всесторонне просмотреть результаты анализа.[боровиков 136] Критерий для определения уровня статистической значимости может быть изменен в поле Alpha (значение по умолчанию 0,05) .[Салманов, с. 254]
Рассмотрим информационную часть окна. В ней содержатся краткие сведения о результатах анализа, а именно:
• Dependent - имя зависимой переменной
• No. of сases - число случаев, по которым построена регрессия
• Multiple R - коэффициент множественной корреляции
• R2 - коэффициент детерминации (квадрат коэффициента множественной корреляции)
• adjusted R2 - скорректированный коэффициент детерминации
• Standard error of estimate - стандартная ошибка оценки
• Intercept - оценка свободного члена регрессии, значение коэффициента В0 в уравнении регрессии.
• Std. Error - стандартная ошибка оценки свободного члена,
стандартная ошибка
коэффициента В0 в уравнении регрессии.
• t(df) and p-value - значение t-критерия и уровень р. t-критерий используется для проверки гипотезы о равенстве 0 свободного члена регрессии.
• F - значения F-критерия.
• df - число степеней свободы F-критерия.
• р - уровень значимости. [боровиков 136-138]
Нажмите на Summary: Regression results на вкладке Quick tab, чтобы отобразить электронную таблицу с бета-коэффициентами (рис. 3).
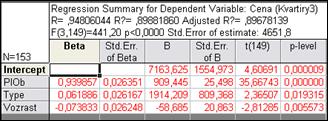
Рис. 3. Таблица коэффициентов уравнения регрессии и оценок их достоверности
Эта электронная таблица показывает стандартизированные бета-коэффициенты регрессии (Beta) и необработанные коэффициенты регрессии (В). Величина этих коэффициентов позволяет сравнивать относительный вклад каждой независимой переменной в предсказании зависимой переменной. Приводится также t-статистика и соответствующее значение вероятности (р) для проверки гипотезы о достоверности этих коэффициентов. [Салманов, с. 254-255]
После того как доказана адекватность модели, полученные результаты можно уверенно использовать для дальнейших действий. Анализ адекватности основывается на анализе остатков. [боровиков 139] Для анализа остатков на вкладке Multiple Regression Results - Residuals/assumptions/prediction tab нажмите кнопку диалога Residual Analysis (рис. 4). [Салманов, с. 256] Здесь имеется возможность рассчитать статистику Дарбина-Уотсона, удаленные остатки, доверительные интервалы для предсказанных значений и многие другие статистики. Широкие возможности анализа остатков и выбросов включают многочисленные типы графиков, диаграмм рассеяния, гистограмм, графики на нормальной и полунормальной вероятностной бумаге и др.[exponenta.ru]
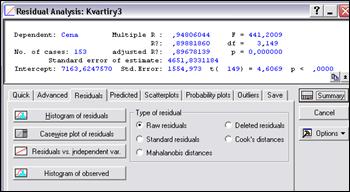
Рис. 4. Окно анализа остатков
Однако можно также применять все аналитические средства STATISTICA, чтобы далее исследовать остатки, создав автономную входную электронную таблицу остатков. [Салманов, с. 261]
3. СОЗДАНИЕ МАКРОСА ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О НОРМАЛЬНОСТИ ОСТАТКОВ
3.1 Описание макроса
При построении модели множественной линейной регрессии особое внимание необходимо уделять проверке гипотезы о нормальном распределении остатков. Это связано с тем, что в условиях нормального распределения остатков оценки параметров модели, построенные методом наименьших квадратов, являются оптимальными. Если распределение отличается от нормального, то свойство оптимальности может быть утрачено. Например, в данных могут быть резко выделяющиеся наблюдения (выбросы), а метод наименьших квадратов чувствителен к выбросам.
В данной курсовой работе осуществлялось эконометрическое моделирование вторичного рынка жилья в г. Минске с использованием статистического пакета Statistica 6.0., обладающего широкими возможностями для построения регрессионных моделей. Пакет Statistica 6.0. содержит встроенный язык программирования VBA, позволяющий создавать дополнительные модули для статистического анализа.
В ходе выполнения множественного регрессионного анализа в модуле Multiple Regression исследование остатков на нормальность можно осуществить лишь графическими методами с использованием нормальных графиков вероятности, доступных из диалога Residual Analysis. Однако на основании графической информации можно сделать лишь предположение о виде распределения остатков. Для проверки остатков на соответствие их нормальному распределению необходимо создать автономную входную электронную таблицу остатков, а затем вызвать модуль Distribution Fitting (Подбор распределения). Нажав кнопку Graph, мы получим результаты применения критерия хи-квадрат, а также гистограмму с проведенной на ней предполагаемой нормальной кривой, на основании которых можно сделать вывод о виде распределения остатков.
Таким образом, при осуществлении множественного регрессионного анализа в пакете Statistica 6.0. необходимо использовать 2 отдельных модуля (Multiple Regression и Distribution Fitting), создавая при этом дополнительную входную электронную таблицу остатков, что требует значительных затрат времени.
Для решения всех вышеперечисленных проблем на языке VBA было написано 2 модуля. Первый модуль (CREATE_MACROS) создает пользовательскую панель инструментов (Приложение Б), а второй (regres-normal) - автоматизирует процесс проверки гипотезы о нормальности остатков регрессии (Приложение А).
После запуска программы CREATE_MACROS, новая панель инструментов CUSTOM будет добавлена к существующей инсталляционной версии STATISTICA. Созданная панель инструментов состоит из 1 главного элемента - кнопки «Нормальность остатков». Чтобы удалить новый элемент панели инструментов, выберите Настройка (Customize) из меню Сервис (Tools) для отображения диалога Настройка (Customize). На вкладке Панели инструментов (Toolbars tab), подсветите новый элемент и Удалите (Delete) его (рис. 1.1).
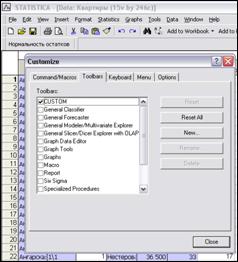
Рис. 1.1. Удаление пользовательской панели инструментов
Для запуска модуля regres-normal необходимо нажать кнопку “Нормальность остатков” на панели инструментов (рис. 1), после чего появится диалог Multiple Regression.Residual Analysis (рис. 2). Критерий для определения уровня статистической значимости может быть изменен в поле Alpha (значение по умолчанию 0,05). При нажатии кнопки Variables отобразится диалог Select dependent and independent variable lists (рис. 3) для выбора зависимой и списка независимых переменных. После нажатия кнопки OK на экране появятся результаты выполнения программы (рис.4).
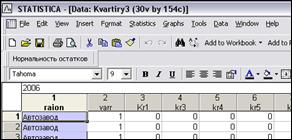
Рис. 1. Кнопка “Нормальностьостатков для запуска модуля

Рис. 2. Стартовая панель модуля
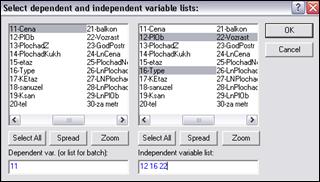
Рис. 3. Окно выбора переменных для анализа
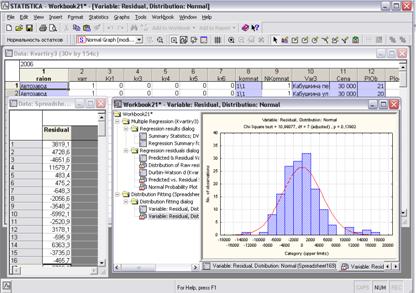
Рис.4. Результаты выполнения программы
Программа вычисляет следующий набор статистик:
1.
Таблицы
результатов оценивания регрессионной модели. Они содержат значения
коэффициентов модели (В), бета-коэффициенты (Beta), их стандартные ошибки, значения
критерия Стьюдента для проверки гипотезы о достоверности этих коэффициентов (![]() и
и ![]() ), коэффициенты корреляции R и детерминации R2,
значение критерия Фишера (F,
p) для проверки гипотезы о достоверности
R и другое.
), коэффициенты корреляции R и детерминации R2,
значение критерия Фишера (F,
p) для проверки гипотезы о достоверности
R и другое.
2. Таблицу результатов анализа остатков, содержащую наблюдаемые (Observed Value) и предсказанные по модели (Predicted Value) значения зависимой переменной, остатки (Residual) и другое.
3. Статистику Дарбина-Уотсона.
4. Графики: гистограмму остатков, диаграмму рассеяния, график на нормальной вероятностной бумаге.
5. Таблицу эмпирических и теоретических частот.
Оба модуля написаны на языке STATISTICA VISUAL BASIC. Рассмотрим схему работы программы regres-normal (рис. 5).
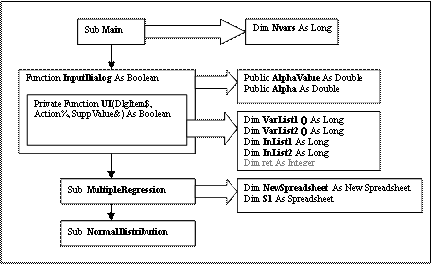

Рис. 5. Схема работы программы regres-normal
Весь блок программного кода в совокупности представляет собой модуль. Модуль regres-normal состоит из ряда операторов, организованных в шесть разделов: это раздел объявлений, начинающийся оператором Option Base 1, процедура Main, функция InputDialog, функция UI, процедуры MultipleRegression и NormalDistribution.
Переменные, содержащиеся в разделе объявлений, представляют собой глобальные переменные (Приложение В, табл. 1). Выполнение программы начинается с процедуры MAIN (рис. 5). Данная процедура вызывает функцию InputDialog, которую в свою очередь обслуживает функция UI. Функция InputDialog отображает пользовательский диалог "Multiple Regression. Residual Analysis", переменные Alpha и AlphaValue инициализируются значениями, содержащимися в соответствующих элементах управления типа TextBox. Функция UI отображает диалог выбора переменных для анализа ("Select dependent and independent variable lists:"). Здесь происходит инициализация списков зависимых и независимых переменных (VarList1(),VarList2()), а также переменных типа Long, хранящих количество элементов в этих списках (InList1, InList2). В случае отсутствия ошибок при вызове пользовательских диалогов далее в процедуре Main происходит последовательный вызов процедур MultipleRegression и NormalDistribution.
В процедуре MultipleRegression осуществляется регрессионный анализ с использованием данных из текущей таблицы (S1), а также происходит инициализация вновь созданной таблицы остатков (NewSpreadsheet). В процедуре NormalDistribution осуществляется проверка остатков из таблицы NewSpreadsheet на нормальное распределение.
3.2 Проверка гипотезы о нормальности остатков в модели вторичного рынка жилья в г. Минске
В модели исследуется зависимость стоимости вторичного жилья в г.Минске (Cena) от следующих факторов: общей площади квартиры (PlOb), возраста дома (Vozrast). Для работы использованы данные о 154 квартирах г. Минска за 2006 год. В модель также включена бинарная, «фиктивная» переменная Type, которая принимает значение 1, если квартира находится в кирпичном доме и значение 0 для всех остальных случаев.
Построенная модель стоимости квартир в г. Минске имеет вид:
![]() (1)
(1)
Все коэффициенты регрессии статистически значимы, что показывает t-статистика и соответствующие значения вероятности (p), которые ниже уровня статистической значимости 0,05.
Для построенной модели
(1) коэффициент корреляции ![]() (значение
близко к 1, что указывает на тесную свяь между зависимой переменной и
факторами). Значение критерия Фишера для проверки гипотезы о достоверности
коэффициента корреляции:
(значение
близко к 1, что указывает на тесную свяь между зависимой переменной и
факторами). Значение критерия Фишера для проверки гипотезы о достоверности
коэффициента корреляции: ![]() ;
;![]() (R достоверно отличен от 0, изучаемый
признак имеет связь хотя бы с одним из регрессоров). Коэффициент детерминации
(R достоверно отличен от 0, изучаемый
признак имеет связь хотя бы с одним из регрессоров). Коэффициент детерминации ![]() , т.е. 90% дисперсии результативного
признака обусловлено влиянием регрессии, а 10% - другими факторами. Анализ
остатков произведён при помощи статистики Дарбина-Уотсона
, т.е. 90% дисперсии результативного
признака обусловлено влиянием регрессии, а 10% - другими факторами. Анализ
остатков произведён при помощи статистики Дарбина-Уотсона ![]() , коэффициент автокорреляции остатков
, коэффициент автокорреляции остатков
![]() . Значит, автокорреляция в остатках
отсутствует.
. Значит, автокорреляция в остатках
отсутствует.
Остатки распределены
нормально: ![]() при
при ![]()
![]()
![]() .
.
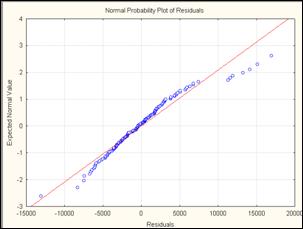
Рис. 1 График остатков на нормальной вероятностной бумаге
На рис. 1 значения по оси y представляют собой функциональное преобразование кривой нормального распределения в прямую. Если наблюдаемые остатки, представленные на оси х, распределяются по нормальному закону, то все значения попадают на прямую линию на графике. В представленном графике остатки расположены достаточно близко к линии, а следовательно можно сделать предположение об их нормальном распределении.
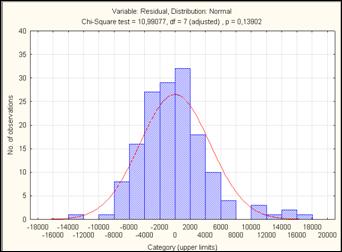
Рис. 2 Гистограмма распределения остатков
Для графической оценки вида распределения также приводится гистограмма распределения остатков (рис.2). Его можно трактовать как соответствующее нормальному.
Рассмотрим график
зависимости остатков εi от теоретических значений
результативного признака ![]() (рис.
3).
(рис.
3).
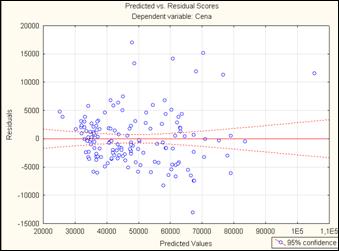
Рис. 3 График зависимости
остатков εi от теоретических значений результативного признака ![]() .
.
Из рисунка 3 можно сделать вывод о наличии гетероскедастичности: остатки εi имеют неодинаковую дисперсию.
Уравнение регрессии имеет наглядную интерпретацию. Так, увеличение общей площади квартиры на 1м2 увеличивает ее цену на 909,445 у.е. Отрицательное значение коэффициента при Vozrast (-58,685) означает, что увеличение возраста квартиры на 1год уменьшает ее цену на 58,685у.е. Квартира в кирпичном доме (Type=1) стоит дороже на 1914,209 у.е., чем аналогичная квартира, например, в панельном доме.
Использование данной модели для прогноза возможно в случае устранения гетероскедастичности, связанной с неоднородностью выборки. Для этого необходимо провести предварительный отбор однородных случаев, а затем осуществить построение модели.
ЗАКЛЮЧЕНИЕ
Математическая статистика и ее применение в экономике - эконометрика - позволяют строить экономические модели и оценивать их параметры, проверять гипотезы о свойствах экономических показателей и формах их связи. В основе методов, с помощью которых строятся экономические модели, лежит корреляционно-регрессионный анализ. Множественный регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой) обусловлено влиянием нескольких независимых величин, а множество всех прочих факторов, также оказывающих влияние на зависимую переменную, принимается за постоянные и средние значения.
Наиболее распространенным в практике статистического оценивания параметров уравнений регрессии является метод наименьших квадратов (МНК). Этот метод основан на ряде предпосылок относительно природы данных и результатов построения модели. Основные из них - это некоррелированность факторов, входящих в уравнение, линейность связи, отсутствие автокорреляции остатков, равенство их математических ожиданий нулю и постоянная дисперсия (гомоскедастичность). Эмпирические данные не всегда обладают такими характеристиками, т.е. предпосылки МНК нарушаются. Применение этого метода в чистом виде может привести к таким нежелательным результатам, как смещение оцениваемых параметров, снижение их состоятельности, устойчивости, а в некоторых случаях может совсем не дать решения. В случае нарушения предпосылок МНК, необходимо корректировать модель.
После оценивания уравнения регрессии по методу наименьших квадратов нужно всегда исследовать остатки на нормальность. В случае нарушения данного предположения модель не является адекватной и не может быть использована для прогнозов.
В пакете STATISTICA имеется внутренний язык программирования Statistica Visual, который добавляет богатый арсенал из более чем 10000 новых функций к стандартному синтаксису Microsoft Visual Basic и является, таким образом, одним из самых функционально богатых и обширных интерфейсов прикладного программирования. SVB также предоставляет широкие возможности по созданию макросов.
В ходе написания данной курсовой работы был создан макрос на языке SVB для проверки гипотезы о нормальности остатков регрессии. Необходимость разработки данного приложения связана с особенностями осуществления регрессионного анализа в пакете STATISTICA. Написанный модуль был использован при эконометрическом моделировании вторичного рынка жилья в г. Минске. Разработанное программное средство может в дальнейшем применятся при построении регрессионных моделей в пакете STATISTICA.
ПРИЛОЖЕНИЕ А
Листинг программы
Option Base 1
Dim S1 As Spreadsheet
Dim NewSpreadsheet As New Spreadsheet
Public AlphaValue As Double
Public Alpha As Double
Dim VarList1 () As Long
Dim VarList2 () As Long
Dim Nvars As Long
Dim InList1 As Long
Dim InList2 As Long
Dim ret As Integer
Sub Main
On Error GoTo NoInputSpreadsheet
Nvars = ActiveDataSet.NumberOfVariables
On Error GoTo Finish
ReDim VarList1(1 To Nvars)
ReDim VarList2(1 To Nvars)
If Not InputDialog Then GoTo Finish
MultipleRegression
NormalDistribution
Finish:
Exit Sub
NoInputSpreadsheet:
MsgBox "Open a data file (Spreadsheet) for this analysis", _
vbCritical
End Sub
Function InputDialog As Boolean
On Error GoTo Finish
InputDialog=False
Begin Dialog UserDialog 390,147, _
"Multiple Regression. Residual Analysis", .UI ' %GRID:10,7,1,1
PushButton 20,14,120,21,"Variables",.VariableSelection
Text 40,42,70,14,"Grouping:",.Text1
Text 110,42,180,14,"none",.Text2
Text 30,56,80,14,"Dependent:",.Text3
Text 110,56,180,14,"none",.Text4
Text 30,84,200,14,"Alpha:",.Text5
TextBox 220,77,90,21,.AlphaValue
Text 30,104,200,14,"Alpha for highlighting effects:",.Text6
TextBox 220,100,90,21,.Alpha
OKButton 310,14,70,21,.OkButton
CancelButton 310,42,70,21,.CancelButton
End Dialog
Dim dlg As UserDialog
dlg.AlphaValue=",05"
dlg.Alpha=",05"
TryAgain:
On Error GoTo Finish
Dialog dlg
On Error GoTo BadAlphaValue
AlphaValue = CDbl(dlg.AlphaValue)
Alpha = CDbl(dlg.Alpha)
InputDialog=True
Finish:
Exit Function
BadAlphaValue:
MsgBox "Bad alpha value; please specify a valid alpha value."
GoTo TryAgain
End Function
Private Function UI(DlgItem$, Action%, SuppValue&) As Boolean
Dim ok As Boolean
Select Case Action%
Case 1 ' Dialog box initialization
Case 2 ' Value changing or button pressed
UI = True
Select Case DlgItem
Case "CancelButton"
UI=False
Case "OkButton"
ok=False
If InList1<1 Or InList2<1 Then
ok=True
GoTo DoVariables
End If
UI=False
Case "VariableSelection"
ok=False
DoVariables:
ret = SelectVariables2 (ActiveDataSet, _
"Select dependent and independent variable lists:", _
1, Nvars, VarList1, InList1, "Dependent var. (or list for batch):", _
1, Nvars, VarList2, InList2, "Independent variable list:")
If ret=0 Then GoTo Finish
If InList1>0 Then
DlgText "Text4", "Selected"
Else
DlgText "Text4", "none"
End If
If InList2>0 Then
DlgText "Text2", "Selected"
Else
DlgText "Text2", "none"
End If
End Select
End Select
Finish:
End Function
Sub MultipleRegression
Set S1 = ActiveSpreadsheet
Dim newanalysis2 As Analysis
Set newanalysis2 = Analysis (scMultipleRegression,S1)
With newanalysis2.Dialog
Variables = Array(VarList1,VarList2)
InputFile = scRegRawData
CasewiseDeletionOfMD = True
PerformDefaultNonStepwiseAnalysis = False
ReviewDescriptiveStatistics = False
ExtendedPrecisionComputations = False
BatchProcessingAndPrinting = False
End With
newanalysis2.Run
With newanalysis2.Dialog
.ComputeConfidenceLimits = True
.AlphaForLimits = AlphaValue
.PLevelForHighlighting = Alpha
End With
newanalysis2.RouteOutput(newanalysis2.Dialog.Summary).Visible = True
newanalysis2.Run
With newanalysis2.Dialog
RawResiduals = True
StandardResidualPlusMinusSigmaOutliers = True
RawPredictedValues = True
MaxNumberOfCasesInSpreadsheetsAndGraphs = 100000
End With
newanalysis2.RouteOutput(newanalysis2.Dialog.Summary).Visible = True
newanalysis2.RouteOutput(newanalysis2.Dialog.HistogramOfResiduals).Visible = True
newanalysis2.RouteOutput(newanalysis2.Dialog.DurbinWatsonStatistics).Visible = True
newanalysis2.RouteOutput(newanalysis2.Dialog.ScatterplotOfPredictedVsResiduals).Visible = True
newanalysis2.RouteOutput(newanalysis2.Dialog.NormalPlotOfResiduals).Visible = True
Set ResSpreadsheetCollection=newanalysis2.Dialog.Summary
Set ResSpreadsheet=ResSpreadsheetCollection.Item(1)
Dim n As Long
n=ResSpreadsheet.NumberOfCases-4
Set Cells=ResSpreadsheet.CellsRange( _
1, 3,n, 3)
Cells.Select
ResSpreadsheet.CopyWithHeaders
NewSpreadsheet.SetSize n, 1
NewSpreadsheet.Visible=True
Set Cells=NewSpreadsheet.CellsRange(1,1,1,1)
Cells.Select
NewSpreadsheet.Paste
End Sub
Sub NormalDistribution
Dim newanalysis3 As Analysis
Set newanalysis3 = Analysis (scDistributions, NewSpreadsheet)
With newanalysis3.Dialog
.FitContinuousDistributions = True
.ContinuousDistribution = scNonNormal
End With
newanalysis3.Run
With newanalysis3.Dialog
Variable = "1"
Distribution = scNonNormal
KolmogorvNo = True
CombineBinsForChiSquare = True
FrequencyDistribution = True
RawFrequencies = True
End With
newanalysis3.RouteOutput(newanalysis3.Dialog.Summary).Visible = True
newanalysis3.RouteOutput(newanalysis3.Dialog.PlotOfDistribution).Visible = True
End Sub
ПРИЛОЖЕНИЕ Б
Листинг программы
Sub Main
Dim bars As CommandBars
Set bars = CommandBarOptions.CommandBars(scBarTypeToolBar)
Dim newBar As CommandBar
Set newBar = bars.Add("CUSTOM")
newBar.InsertMacroButton 1, "d:\work\Macros\_1_\regres-normal.svb" , "Нормальность остатков"
newBar.InsertSeparator 2
newBar.Item(1).DisplayMode = scCommandDisplayTextAndImage
End Sub
ПРИЛОЖЕНИЕ В
Таблица 1
Глобальные переменные
| Переменные | Описание переменных | Значение переменных |
| Dim S1 As Spreadsheet | Объект таблица | Текущая таблица |
| Dim NewSpreadsheet As New Spreadsheet | Объект таблица | Таблица для остатков |
| Public AlphaValue As Double | Переменная типа Double | |
| Public Alpha As Double | Переменная типа Double | |
| Dim VarList1() As Long | Динамический массив типа Long | Список зависимых переменных |
| Dim VarList2() As Long | Динамический массив типа Long | Список независимых переменных |
| Dim Nvars As Long | Переменная типа Long | Количество переменных в текущей таблице |
| Dim InList1 As Long | Переменная типа Long | Номера зависимых переменных |
| Dim InList2 As Long | Переменная типа Long | Номера независимых переменных |
| Dim ret As Integer | Переменная типа Integer |