Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Учебное пособие: Теория вероятностей и математическая статистика
Учебное пособие: Теория вероятностей и математическая статистика
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
высшего профессионального образования
«Южный Федеральный университет»
Факультет математики, механики и компьютерных наук
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
учебной дисциплины
«Теория вероятностей и математическая статистика»
для бакалавров
вузовского компонентного цикла ОПД
по специальности 010501
«Прикладная математика и информатика»
Рассмотрено и рекомендовано УТВЕРЖДАЮ
на заседании кафедры Декан факультета
теории функций и
функционального анализа ЮФУ
Протокол №____ _________________
«___»________2008 г.
«___»________2008 г.
Зав кафедрой ____________ (Кондаков В.П.)
Составитель:
доцент кафедры Луценко А.И.
Ростов-на-Дону
2008
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
I. Цели и задачи дисциплины, ее место в учебном процессе
I.1 Цели преподавания дисциплины
Курс «Теория вероятностей и математическая статистика» - общеобразовательная математическая дисциплина, объектом изучения которой является большая область математики, связанная понятиями случайности событий, измерением степени возможности появления этих событий, проведением экспериментальных исследований и математической обработкой их результатов, формулировкой полученных результатов.
Курс «Теория вероятностей и математическая статистика» читается студентам специальности “прикладная математика и информатика” в VI и VII семестрах. Цель преподавания – ознакомить студентов с задачами и методами теории вероятностей и математической статистики в объёме, достаточном для успешного практического использования полученных знаний в дальнейшей работе по специальности, а также для самостоятельного изучения соответствующей научной литературы.
I.2 Задачи изучения дисциплины
В результате изучения настоящего курса студент должен:
1) овладеть основами теории вероятностей, усвоив понятия множества элементарных исходов, алгебры случайных событий, вероятностной функции как числовой функции множеств, случайной величины, функции распределения случайной величины и числовых характеристик случайной величины;
2) ознакомится с методами и результатами решения классической предельной проблемы теории вероятностей, а также с применением этих результатов к решению задач статистической оценки значений числовых характеристик случайных величин и векторов и статистической проверки гипотез, построению простейших регрессионных моделей;
3) приобрести навыки практического решения вероятностных задач, постановки задач проведения статистического эксперимента, научится приёмам и методам статистической обработки экспериментальных данных и формулированию обоснованных выводов по результатам этой обработки.
I.3 Перечень дисциплин с указанием разделов (тем), знание которых необходимо для изучения теории вероятностей и математической статистики
1) Элементы теории множеств (операции над множествами, конечные и бесконечные множества, сравнение бесконечных множеств по мощности, алгебра множеств);
2) Математический анализ (теория пределов, непрерывные и дифференцируемые функции, ряды, преобразование Фурье);
3) Теория функций и функциональный анализ (понятия меры и измеримости множеств, интеграла Лебега, гильбертова пространства, различных видов сходимости последовательностей).
Согласно государственного образовательного стандарта высшего профессионального образования от 14 апреля 2000 года на изучение дисциплины «Теория вероятностей и математическая статистика» отведено 280 часов (70 часов лекционных + 35 часов практических аудиторных занятий + 175 часов самостоятельной работы) и предусмотрены следующие формы отчётности: 1 экзамен, 1 зачёт, 3 контрольных работы и 1 зачётное индивидуальное задание по математической статистике.
II. Рабочая программа курса
Модуль 1. Вероятностное пространство с не более чем счетным множеством элементарных исходов
Основные понятия: Элементарный исход. Множество элементарных исходов. Алгебра событий. Вероятностная функция. Условная вероятность.
Вероятностное пространство <W,A,P>
|
Множество элементарных исходов W |
Алгебра событий A |
Вероятностная функция P |
| Примеры | Операции над событиями | Простейшие свойства |
1. Классическая модель: ![]() ;
;
(Урновая схема, различные способы организации выборок).
2. Биномиальная модель (Схема Бернулли):
![]() ;
;
(Полиномиальная модель).
3. Геометрическая модель: ![]() ;
;
(Отрицательное биномиальное распределение).
Условная вероятность. Попарная независимость событий и независимость событий в совокупности.
Формула полной вероятности. Формула Байеса. (7 часов)
Модуль 2. Общая вероятностная модель. Аксиоматика А.Н. Колмогорова
Основные понятия: σ-алгебра множеств. Измеримое пространство. σ-аддитивная функция множеств. Нормированная функция множеств. Бесконечные множества различной мощности.
Аксиоматическое построение вероятностного пространства <W, A, P >. Свойства вероятностной функции. Борелевские алгебры множеств. Измеримые пространства <R, B (R)>; <Rn, B (Rn)>. Типы и примеры задания вероятностных функций на измеримых пространствах. (6 часов)
Модуль 3. Случайные величины и векторы
Основные понятия: Измеримая функция. Ряд распределения. Плотность вероятности. Компоненты случайного вектора. Согласованность законов распределения вероятностей. Устойчивость законов распределения вероятностей.
Случайная величина - измеримое отображение <W,A > в <R, B (R)>.
Случайный вектор - измеримое отображение <W,A > в <Rn, B (Rn)>.
Типы случайных величин и векторов. Задание законов распределения. Функция распределения случайной величины и случайного вектора. Компоненты случайного вектора. Частные распределения и частные функции распределения. Многомерный нормальный закон. Составной случайный вектор. Независимость случайных величин. Критерий независимости (три формы).
(9 часов)
Модуль 4. Числовые характеристики случайных величин и векторов
Основные понятия: Функция случайной величины. Математическое ожидание. Дисперсия. Начальные и центральные моменты случайных величин и векторов. Ковариационный момент. Коэффициент линейной корреляции.
Интеграл Лебега-Стилтьеса (Римана-Стилтьеса). Математическое ожидание случайной величины и случайного вектора. Свойства. Примеры. Дисперсия случайной величины. Свойства. Примеры. Начальные и центральные моменты случайной величины и случайного вектора. Ковариационный момент. Ковариационная матрица. Коэффициент линейной корреляции и его свойства. Условные распределения и условные математические ожидания. Линейная регрессия случайных величин. (12 часов)
Модуль 5. Классическая предельная проблема теории вероятностей
Основные понятия: Центрированные и нормированные суммы случайных величин. Виды сходимостей последовательностей случайных величин. Схема серий. Асимптотическая малость последовательности случайных величин.
Характеристические функции. Определение. Примеры характеристических функций для некоторых законов распределения случайных величин. Свойства характеристических функций. Теоремы непрерывности для последовательностей функций распределения и характеристических функций.
Классическая предельная проблема теории вероятностей
| ЗБЧ | ЦПТ | ЗМЧ |
|
Теорема Бернулли Теорема Хинчина Теорема Чебышева Теорема Пуассона |
Теорема Муавра- Лапласа Теорема Леви Теорема Ляпунова Теорема Линдеберга-Феллера |
Теорема Пуассона |
У З Б Ч: Теорема Бореля и теорема Кантелли. Теоремы Колмогорова. Метод Монте-Карло. (10 часов)
Модуль 6. Первичная обработка статистических данных. Точечные оценки числовых характеристик
Основные понятия: Выборка. Вариационный ряд. Гистограмма. Состоятельность, несмещенность, эффективность точечных оценок. Статистика.
Требования к организации выборки. Первичная обработка статистических данных. Теорема Гливенко. Достаточные статистики. Точечные оценки числовых характеристик случайных величин. Требования к точечным оценкам. Неравенство Рао-Крамера. Методы получения точечных оценок числовых характеристик. (8 часов)
Модуль 7. Интервальные оценки числовых характеристик
Основные понятия: Степень
свободы. Доверительная вероятность. Распределение Пирсона (![]() распределение). Распределение
Стьдента (
распределение). Распределение
Стьдента (![]() распределение).
Распределение Фишера-Снедекора (
распределение).
Распределение Фишера-Снедекора (![]() распределение).
распределение).
Доверительный интервал. Специальные распределения. Общая линейная модель измерений. Распределения некоторых статистик. Примеры построения доверительных интервалов для числовых характеристик случайных величин. (4 часа)
Модуль 8. Статистическая проверка гипотез
Основные понятия: Гипотеза. Критерий проверки гипотезы. Уровень значимости гипотезы. Критическая область. Правило принятия решений. Оптимальный критерий проверки гипотезы.
Гипотезы основная и
альтернативная. Критерий проверки гипотезы. Распределения вероятностей критерия
проверки гипотезы. Области ![]() и
и ![]() возможных значений
критерия при справедливости основной гипотезы. Ошибки I и II рода при проверке
гипотез. Оптимальный критерий. Три типа задач статистической проверки гипотез. Примеры
построения критериев для статистической проверки гипотез. (6 часов)
возможных значений
критерия при справедливости основной гипотезы. Ошибки I и II рода при проверке
гипотез. Оптимальный критерий. Три типа задач статистической проверки гипотез. Примеры
построения критериев для статистической проверки гипотез. (6 часов)
Модуль 9. Корреляционный и регрессионный анализы
Основные понятия: Статистическая зависимость компонент случайного вектора. Сила и характер статистической зависимости компонент случайного вектора. Условные случайные величины. Условные законы распределения вероятностей и условные математические ожидания. Функция регрессии.
Корреляция и регрессия случайных величин. Две задачи, решаемые корреляционным анализом. Коэффициент линейной корреляции и его статистическая оценка. Проверка гипотезы о значимости коэффициента линейной корреляции. Условное математическое ожидание. Функция регрессии. Функция регрессии двумерного нормального закона. Определение статистических оценок коэффициентов функции регрессии. Остаточная дисперсия. Корреляционное отношение. (6 часов)
Распределение часов по видам учебной нагрузки
| № | Модуль |
Общее кол-во часов |
Лекции |
Практ. занятия |
Самост- ная работа |
| 1 |
Вероятностное пространство с не более чем счётным множеством элементарных исходов |
33 | 7 | 6 | 20 |
| 2 | Общая вероятностная модель. Аксиоматика А.Н. Колмогорова | 18 | 6 | 2 | 10 |
| 3 |
Случайные величины и векторы |
31 | 9 | 6 | 16 |
| 4 |
Числовые характеристики случайных величин и векторов |
37 | 12 | 6 | 19 |
| 5 |
Классическая предельная проблема теории вероятностей |
29 | 12 | 5 | 12 |
| 6 |
Первичная обработка статистических данных. Точечные оценки числовых характеристик |
18 | 8 | 4 | 6 |
| 7 |
Интервальные оценки числовых характеристик |
10 | 4 | 2 | 4 |
| 8 | Статистическая проверка гипотез | 18 | 6 | 2 | 10 |
| 9 |
Корреляционный и регрессионный анализ |
16 | 6 | 2 | 8 |
| Всего | 210 | 70 | 35 | 105 |
Рекомендуемая литература
1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983.
2. Боровков А.А. Курс теории вероятностей. - М.: Наука, 1986.
3. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1973.
4. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. – М.: Высшая школа, 2000.
5. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1988.
6. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1977.
7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 1979.
8. Драгилев М.М. Теория вероятностей. М.: Вузовская книга, 2002.
9. Кожевников Ю.В. Теория вероятностей и математическая статистика. – М.: Машиностроение, 2002.
10.Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1991.
11.Крамер Г. Математические методы статистики. - М.: Мир, 1975.
12.Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. - М.: Наука, 1975.
13.Мешалкин Л.Ф. Сборник задач по теории вероятностей. - Издательство Московского университета, 1963.
14.Сборник задач по теории вероятностей, математической статистике и теории случайных функций, под редакцией Свешникова А.А. – М.:Наука, 1970.
15.Севастьянов Б.А., Курс теории вероятностей и математической статистики. – М.; Наука, 1982.
16.Севастьянов Б.А., Чистяков В.П., Зубков Ф.М. Сборник задач по теории вероятностей. - М.: Наука, 1980.
17.Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. - М.: Физматгиз, 1980.
18.Феллер В. Введение в теорию вероятностей и ее приложения. В 2-х томах - М.: Мир, 1984.
19.Чистяков В.П. Курс теории вероятностей. - М.: Наука, 1982.
20.Ширяев А.Н. Вероятность. – М.: Наука, 1980.
Практическая (аудиторная) часть
70 часов аудиторных занятий + 70 часов самостоятельной работы + 3 контрольных работы + 1 индивидуальное задание по математической статистике.
3 курс, шестой семестр. (36 часов)
1. Классическое определение вероятности. 4 часа
2. Вероятности сумм и произведений событий. 4 часа
3. Формула полной вероятности. 2 часа
4. Формула Байеса. 2 часа
5. Повторные независимые испытания. Формула Бернулли. 2 часа
6. Контрольная работа №1. 2 часа
7. Геометрические вероятности. 4 часа
8. Дискретная случайная величина. Ряд распределения 4 часа
Функция распределения.
9. Числовые характеристики дискретной случайной величины. 4 часа
10. Непрерывная случайная величина. Плотность вероятности. 2 часа
Функция распределения.
11. Числовые характеристики непрерывной случайной величины. 4 часа
12. Контрольная работа №2. 2 часа
4 курс, седьмой семестр. (34 часа)
1. Повторение. Дискретные и непрерывные случайные величины и их числовые характеристики. 4 часа
2. Нормальный закон. Функция Лапласа. 2 часа
3. Интегральная теорема Муавра-Лапласа и ее приложения. 4 часа 5.Закон больших чисел и Центральная предельная теорема. 4 часа
6.Функции случайных величин и их числовые характеристики. 4 часа
7.Контрольная работа №3. 2 часа
8. Первичная обработка статистических данных. 2 часа
9.Точечные оценки числовых характеристик случайных величин. 2 часа
10. Доверительные интервалы для математического ожидания и дисперсии.
2 часа
11. Статистическая проверка гипотез. Задачи I-го и II-го типов. 4 часа
12. Критерий согласия Пирсона. 2 часа
13. Корреляционный анализ. 4 часа
Литература:
1 А.А. Свешников Сборник задач по теории вероятностей, математической статистике и теории случайных функций. Москва. “Наука”. 1970г.
2. А.И. Луценко Задачи по теории вероятностей. Часть I, УПЛ РГУ. 2005г.
3. А.И. Луценко Задачи по теории вероятностей. Часть II, УПЛ РГУ. 2001г.
4. В.Е. Ковальчук, А.И. Луценко Индивидуальные задания по математической статистике. УПЛ РГУ. 1998г.
III. Контрольные вопросы
Модуль 1. Вероятностное пространство с не более чем счётным множеством элементарных исходов
1. Могут ли два различных элементарных исхода одновременно произойти в результате проведения испытания.
2. Сколько элементов будет иметь алгебра событий, если множество элементарных исходов состоит из n элементов?
3. Запишите случайное событие,
являющееся противоположным событием случайному событию ![]() .
.
4. Запишите случайное событие,
являющееся противоположным событием случайному событию ![]() .
.
5. Вероятности наступления случайных
событий ![]() и
и ![]() равны
равны ![]() и
и ![]() . Будут ли эти события
несовместными?
. Будут ли эти события
несовместными?
6. Сколько элементов будет иметь алгебра событий, «порождаемая» случайными событиями A и B?
7. Повторные независимые испытания проводятся n раз. В результате каждого испытания может произойти только одно из трёх попарно несовместных событий A, B или C. Определите элементарный исход для таких испытаний. Сколько элементов будет иметь множество элементарных исходов?
8. Будут ли гипотезы, формулируемые при применении формулы полной вероятности, попарно независимыми событиями?
9. Может ли сумма всех послеопытных вероятностей гипотез, вычисленных по формуле Байеса, быть меньше единицы?
10. Проводятся одинаковые независимые испытания до тех пор, пока событие A не появится три раза. Сколько элементарных исходов будет благоприятствовать случайному событию: «Было проведено десять испытаний»?
Модуль 2. Общая вероятностная модель. Аксиоматика А.Н. Колмогорова
1. Удовлетворяет ли условию: ![]() аддитивная числовая функция
множеств
аддитивная числовая функция
множеств ![]() для любых
для любых![]() и
и ![]() , если
, если ![]() ?
?
2. Будет ли всегда справедливо равенство
![]() , если
, если ![]() ?
?
3. Будет ли требование аддитивности числовой функции множеств аксиоматическим, если рассматриваются испытания, для которых множество элементарных исходов имеет не более чем счётное число элементов?
4. Может ли алгебра всех возможных событий быть множеством счётной мощности, если множество элементарных исходов имеет конечное число элементов?
5. Можно ли построить алгебру событий, имеющую счётное число элементов, если множество элементарных исходов – счётное?
6. Будут ли совпадать σ-алгебры
борелевских множеств B1(R) и B2(R), если
первая алгебра построена по элементам системы ![]() ,
где
,
где ![]() и
и ![]() - любые действительные
числа, а вторая алгебра построена по элементам системы
- любые действительные
числа, а вторая алгебра построена по элементам системы ![]() , где
, где ![]() и
и ![]() - любые рациональные
числа?
- любые рациональные
числа?
7. Может ли вероятностная функция быть линейной комбинацией двух вероятностных функций, одна из которых – дискретного, а другая - непрерывного типа?
8. Из «непрерывности снизу» вероятностной функции следует её «непрерывность в нуле». Можно ли утверждать, что из «непрерывности в нуле» следует «непрерывности снизу» вероятностной функции?
9. Вероятностная функция P определена на измеримом пространстве <![]() , B (
, B (![]() )>. Может ли первая частная
вероятностная функция
)>. Может ли первая частная
вероятностная функция ![]() быть
дискретного типа, а вторая частная вероятностная функция
быть
дискретного типа, а вторая частная вероятностная функция ![]() быть непрерывного
типа?
быть непрерывного
типа?
10. Произвольная функция ![]() определена на
интервале
определена на
интервале ![]() и принимает неотрицательные
значения. Что нужно сделать, что бы её можно было назвать вероятностной
функцией, определённой на интервале
и принимает неотрицательные
значения. Что нужно сделать, что бы её можно было назвать вероятностной
функцией, определённой на интервале ![]() ?
?
Модуль 3. Случайные величины и векторы
1. Можно ли утверждать, что случайная величина есть случайный результат любого опыта?
2. Можно ли утверждать, что плотность
вероятности ![]() это любая функция, для
которой справедливо
это любая функция, для
которой справедливо 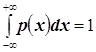 ?
?
3. Как по заданной функции распределения
![]() определить распределение
вероятностей
определить распределение
вероятностей ![]() , где
, где ![]() , случайной величины
, случайной величины ![]() ?
?
4. Как по заданной функции распределения
![]() определить плотность
вероятности
определить плотность
вероятности ![]() случайной величины
случайной величины ![]() ?
?
5. Как, зная плотность вероятности ![]() двумерной случайной
величины
двумерной случайной
величины ![]() , определить частную функцию
распределения
, определить частную функцию
распределения ![]() второй
компоненты
второй
компоненты ![]() ?
?
6. Какому требованию должны
удовлетворять компоненты двумерной случайной величины ![]() , чтобы было справедливо
равенство
, чтобы было справедливо
равенство ![]() ?
?
7. Может ли у двумерной случайной
величины ![]() одна компонента быть
случайной величиной дискретного типа, а другая - случайной величиной
непрерывного типа?
одна компонента быть
случайной величиной дискретного типа, а другая - случайной величиной
непрерывного типа?
8. Рассматривается вероятностное
пространство <W,A,P>, где P - вероятностная функция непрерывного типа. Можно ли
на измеримом пространстве <W,A>
определить случайную величину ![]() , у
которой функция распределения
, у
которой функция распределения ![]() будет
функцией распределения дискретного типа?
будет
функцией распределения дискретного типа?
9. Всегда ли по частным функциям
распределения компонент ![]() и
и ![]() можно определить функцию
распределения двумерной случайной величины
можно определить функцию
распределения двумерной случайной величины ![]() ?
?
10. Как, зная функцию распределения
случайного вектора ![]() определить
функцию распределения случайного вектора
определить
функцию распределения случайного вектора ![]() ?
?
Модуль 4. Числовые характеристики случайных величин и векторов
1. Почему, определяя математическое
ожидание функции случайной величины ![]() как
значение несобственного интеграла
как
значение несобственного интеграла ![]() , мы
требуем, чтобы этот интеграл сходился абсолютно?
, мы
требуем, чтобы этот интеграл сходился абсолютно?
2. Если справедливо равенство ![]() , то можно ли утверждать,
что распределение вероятностей случайной величины
, то можно ли утверждать,
что распределение вероятностей случайной величины ![]() будет
симметрично относительно математического ожидания?
будет
симметрично относительно математического ожидания?
3. Случайная величина ![]() имеет конечное математическое
ожидание
имеет конечное математическое
ожидание ![]() . Следует ли из этого, что
у случайной величины
. Следует ли из этого, что
у случайной величины ![]() существует
конечная дисперсия
существует
конечная дисперсия ![]() ?
?
4. Случайная величина ![]() имеет конечную дисперсию
имеет конечную дисперсию ![]() . Следует ли из этого, что
у случайной величины
. Следует ли из этого, что
у случайной величины ![]() существует
конечное математическое ожидание
существует
конечное математическое ожидание ![]() ?
?
5. Используя свойства дисперсии, докажите что:
а) ![]() , если случайные величины
, если случайные величины ![]() и
и ![]() - независимые;
- независимые;
б) ![]() , где c – произвольная константа.
, где c – произвольная константа.
6. Используя определения начальных и центральных моментов двумерной случайной величины, запишите формулу дисперсии суммы двух произвольных случайных величин.
7. Если случайные величины ![]() и
и ![]() - независимые, то ковариационный
момент
- независимые, то ковариационный
момент ![]() всегда равен нулю. Будет ли
справедливо обратное утверждение: если ковариационный момент случайных величин
всегда равен нулю. Будет ли
справедливо обратное утверждение: если ковариационный момент случайных величин ![]() и
и ![]() равен нулю, то случайные
величины
равен нулю, то случайные
величины ![]() и
и ![]() - независимые?
- независимые?
8. Можно ли утверждать, что значение математического ожидания случайной величины - это наиболее вероятное значение случайной величины?
9. Всегда ли равенство нулю коэффициента линейной корреляции свидетельствует об отсутствии статистической связи между случайными величинами?
10. В ковариационной матрице n-мерного случайного вектора ненулевыми являются только элементы, стоящие на главной диагонали. Что можно сказать о компонентах этого вектора?
Модуль 5. Классическая предельная проблема теории вероятностей
1. Какой вид сходимости последовательности случайных величин сильнее: сходимость по распределению, или сходимость по вероятности?
2. Какое требование к последовательностям случайных величин предъявляется во всех теоремах классической предельной проблемы теории вероятностей?
3. Можно ли применять теорему Хинчина к последовательностям одинаково распределённых случайных величин, имеющих конечные дисперсии?
4. Покажите, что теорема Муавра-Лапласа является частным случаем теоремы Леви.
5. Последовательность независимых одинаково распределённых случайных величин подчиняется ЦПТ. Можно ли утверждать, что эта последовательность подчиняется ЗБЧ?
6. Последовательность независимых разно распределённых случайных величин подчиняется ЗБЧ. Можно ли утверждать, что эта последовательность подчиняется ЦПТ?
7. Можно ли утверждать, что теорема Хинчина является частным случаем теоремы Чебышева?
8. Покажите, что из того, что последовательность случайных величин подчиняется условию Ляпунова следует, что она подчиняется и условию Линдеберга.
9. Покажите, что теорема Муавра-Лапласа является частным случаем теоремы Линдеберга?
10. Покажите, что последовательность независимых разно распределённых бернуллиевских случайных величин подчиняется ЦПТ.
Модуль 6. Первичная обработка статистических данных. Точечные оценки числовых характеристик
1. Каким условием надо руководствоваться для определения числа интервалов при построении вариационного ряда?
2. Могут ли интервалы вариационного ряда иметь разные длины?
3. Можно ли утверждать, что из несмещённости точечной оценки числовой характеристики следует е состоятельность?
4. Будет ли точечная оценка, полученная методом максимального правдоподобия несмещённой оценкой числовой характеристики?
5. Какая теорема применяется при проверке состоятельности точечных оценок начальных моментов исследуемой случайной величины?
6. Может ли точечная оценка дисперсии быть отрицательным числом?
7. При проверке состоятельности оценки ![]() применяется лемма, в
которой по непрерывной функции
применяется лемма, в
которой по непрерывной функции ![]() строится
сходящаяся по вероятности последовательность
строится
сходящаяся по вероятности последовательность ![]() ,
,
![]() . Точечной оценкой
коэффициента линейной корреляции будет статистика
. Точечной оценкой
коэффициента линейной корреляции будет статистика 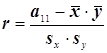 , получаемая методом
моментов. Постройте непрерывную функцию, с помощью которой, применяя лемму,
можно проверить состоятельность этой оценки.
, получаемая методом
моментов. Постройте непрерывную функцию, с помощью которой, применяя лемму,
можно проверить состоятельность этой оценки.
8. У случайной величины отсутствует математическое ожидание. Имеется статистическая выборка значений этой случайной величины. Можно ли утверждать, что у элементов выборки существует конечное среднее арифметическое?
9. Можно ли утверждать, что увеличение объёма выборки приводит к уменьшению величины отличия получаемых значений средних арифметических от значения математического ожидания?
10. Можно ли применять неравенство Рао-Крамера для проверки несмещённости точечной оценки?
Модуль 7. Интервальные оценки числовых характеристик
1. Увеличение объёма выборки при неизменном значении доверительной вероятности приводит к уменьшению длины доверительного интервала. Как будет изменяться доверительная вероятность, если при постоянной длине доверительного интервала будет увеличиваться объём выборки?
2. Покажите, что при увеличении числа n последовательность случайных величин
![]() сходится по распределению к
нормальному закону.
сходится по распределению к
нормальному закону.
3. Покажите, что при увеличении числа n последовательность случайных величин
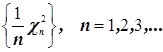 сходится по вероятности к
единице.
сходится по вероятности к
единице.
4. Как изменяется длина доверительного интервала при увеличении доверительной вероятности?
5. Известно, что исследуемая случайная
величина подчиняется нормальному закону с параметрами m и ![]() .
Можно ли использовать в качестве доверительных интервалов интервалы
.
Можно ли использовать в качестве доверительных интервалов интервалы ![]() , где
, где ![]() ? Чему будут равны
доверительные вероятности
? Чему будут равны
доверительные вероятности ![]() ?
?
Модуль 8. Статистическая проверка гипотез
1. Что называется критерием статистической проверки гипотез?
2. Можно ли выбрать такой критерий, при котором вероятность ошибки первого рода будет равна нулю?
3. Какие распределения вероятностей используются при построении критерия статистической проверки гипотез?
4. Дайте формулировку правила принятия решений?
5. Сколько типов задач рассматривается методами статистической проверки гипотез?
6. По результатам проверки двух гипотез:
![]() ,
,
![]() ,
,
где ![]() и
и ![]() - разные функции
распределения, по элементам одной и той же выборки, прияты решения о том, что
нет оснований отклонять и первую, и вторую гипотезу.
- разные функции
распределения, по элементам одной и той же выборки, прияты решения о том, что
нет оснований отклонять и первую, и вторую гипотезу.
Может ли встретится такая ситуация при применении критерия Пирсона?
7. Может ли увеличение объёма выборки, по которой вычисляется наблюдаемое значение критерия, привести к отмене ранее принятого решения об отклонении основной гипотезы?
8. Можно ли использовать одну и ту же выборку для проверки гипотезы о значении математического ожидания и гипотезы о виде закона распределения исследуемой случайной величины?
9. В результате проверки принято решение об отклонении основной гипотезы и принятии альтернативной гипотезы.
Затем основную гипотезу
назвали альтернативной, а альтернативную гипотезу назвали основной. Для того же
критерия ![]() , при том же уровне
значимости α определены новые области
, при том же уровне
значимости α определены новые области ![]() и
и
![]() . Какое решение будет принято,
если будет использована та же выборка?
. Какое решение будет принято,
если будет использована та же выборка?
10. Можно ли проверку знаний студента на экзамене считать статистической проверкой гипотез? Сформулируйте основную и альтернативную гипотезы. Что будет являться критерием проверки справедливости основной гипотезы? Объясните причины ошибок первого и второго рода.
Модуль 9. Корреляционный и регрессионный анализы
1. Какие задачи решаются в корреляционном анализе?
2. Может ли статистическая оценка коэффициента линейной корреляции принимать значения, модуль которых будет больше единицы?
3. В каком случае условные распределения компонент случайного вектора будут совпадать с частными распределениями компонент?
4. Какой вид будут иметь функции регрессии каждой из компонент случайного вектора, если эти компоненты независимые случайные величины?
5. Определите координаты точки пересечения линейных уравнений регрессии компонент двумерной случайной величины.
6. При каком условии на компоненты двумерной случайной величины функции линейной регрессии одной компоненты на другую будут тождественно совпадать?
7. Чему будут равны остаточные дисперсии компонент двумерной случайной величины, если эти компоненты будут независимыми?
8. Чему будут равны остаточные дисперсии компонент двумерной случайной величины, если эти компоненты будут связаны линейной функциональной зависимостью?
9. Какой критерий применяется при проверке значимости коэффициента линейной корреляции?
10. В чём заключается различие между корреляционным и регрессионным анализами?
.
IV. Методические указания
Модуль 1. Вероятностное пространство с не более чем счетным множеством элементарных исходов
Цель модуля: Студент должен ознакомиться с основными понятиями и определениями теории вероятностей. Научиться решать задачи определения вероятностей наступления событий для простейших моделей испытаний, предусматривающих построение не более чем счётного множества элементарных исходов.
Введение основных понятий теории вероятностей, базируется на договоре о существе содержания терминов, на которых базируется новый предмет. Это понятия: испытание, элементарный исход, множество элементарных исходов, благоприятствующие элементарные исходы, равновозможные элементарные исходы. Усвоение этих основных понятий обеспечивается только жизненным опытом и способностью к абстрактному мышлению.
После ознакомления с основными понятиями, формулируется первые основные определения теории вероятностей. Это определения случайного события, противоположного события, достоверного и невозможного события, суммы и произведения событий, совместных и несовместных событий, алгебры событий.
После ознакомления с основными понятиям и усвоения основныхе определений, проводится подготовка к знакомству с новым, важнейшим понятием курса – понятием вероятности случайного события. Делается это аксиоматически, путем введения вероятностной функции Р.
Вероятностная функция P вводится следующим образом.
Сначала постулируется,
аксиоматически формулируется: «Каждому элементарному исходу ![]() некоторым разумным
способом ставим в соответствие положительное число
некоторым разумным
способом ставим в соответствие положительное число ![]() ,
(записывается это так:
,
(записывается это так: ![]() ). При этом
требуется, чтобы выполнялось условие:
). При этом
требуется, чтобы выполнялось условие: ![]() .»
Затем, с использованием понятия благоприятствующего случайному событию элементарного
исхода, определяется вероятность наступления случайного события следующим
образом:
.»
Затем, с использованием понятия благоприятствующего случайному событию элементарного
исхода, определяется вероятность наступления случайного события следующим
образом: ![]() . То есть, по существу,
каждому элементу A алгебры A, A
. То есть, по существу,
каждому элементу A алгебры A, A![]() A, ставится в
соответствие неотрицательное число, которое называется вероятностью этого
элемента – вероятностью
A, ставится в
соответствие неотрицательное число, которое называется вероятностью этого
элемента – вероятностью ![]() наступления
случайного события A.
То есть вводится функция, которая отображает множество A во множество чисел сегмента
наступления
случайного события A.
То есть вводится функция, которая отображает множество A во множество чисел сегмента ![]() . Кратко это можно записать
так: P: A
. Кратко это можно записать
так: P: A![]() . Так как здесь нельзя, подобно тому
как это делается в анализе, ввести вероятностную функцию Р с помощью
аналитической записи типа
. Так как здесь нельзя, подобно тому
как это делается в анализе, ввести вероятностную функцию Р с помощью
аналитической записи типа ![]() :
:![]() , то у студента на этом
этапе изучения курса возникают трудности в осмыслении понятия вероятностная
функция.
, то у студента на этом
этапе изучения курса возникают трудности в осмыслении понятия вероятностная
функция.
Для облегчения процесса понимания
термина «вероятность случайного события», мы прибегаем к механической
интерпретации. Установление соответствия ![]() интерпретируется
как распределение по элементам
интерпретируется
как распределение по элементам ![]() множества
W некоторым разумным способом
единичной массы: в каждом
множества
W некоторым разумным способом
единичной массы: в каждом ![]() мы
помещаем” массу равную
мы
помещаем” массу равную ![]() .
Вероятность случайного события A теперь понимается как доля единичной массы, оказавшейся над подмножеством
А множества W.
.
Вероятность случайного события A теперь понимается как доля единичной массы, оказавшейся над подмножеством
А множества W.
Слова «некоторым разумным
способом устанавливаем соответствие ![]() » своей
неопределенностью вносят дополнительные трудности в понятие термина «введение
вероятностной функции» и нуждаются в пояснениях. Эти пояснения даются путем рассмотрения
трёх моделей, трёх конкретных типов испытаний, в которых это соответствие
устанавливается вполне естественным, разумным способом.
» своей
неопределенностью вносят дополнительные трудности в понятие термина «введение
вероятностной функции» и нуждаются в пояснениях. Эти пояснения даются путем рассмотрения
трёх моделей, трёх конкретных типов испытаний, в которых это соответствие
устанавливается вполне естественным, разумным способом.
Классическая модель,
основанная на понятии «испытаний с равновозможными элементарными исходами», позволяет
установить соответствие так: ![]() .
.
Биномиальная модель,
основанная на понятии «серии повторных независимых испытаний», позволяет
установить соответствие так: ![]() .
.
Геометрическая модель,
основанная на понятии «последовательность повторных независимых испытаний до
первого положительного исхода», позволяет установить соответствие так: ![]() .
.
Перед рассмотрением
биномиальной модели сначала вводится понятие «случайного события B наступившего при условии, что
экспериментатору известно, что событие A уже произошло» и формулируется определение условной
вероятности ![]() . Затем рассматривается
вероятность произведения событий и формулируется одно из фундаментальных
определений теории – определение независимости событий.
. Затем рассматривается
вероятность произведения событий и формулируется одно из фундаментальных
определений теории – определение независимости событий.
Свойства вероятностной функции, а так же формулы полной вероятности и Байеса являются теоремами и следствиями, вытекающими из аксиоматического введения вероятностной функции P, и позволяют решать на практических занятиях довольно широкий круг задач.
Модуль 2. Построение общей вероятностной модели
Аксиоматика А.Н. Колмогорова.
Цель модуля: Узнать принцип построения общей вероятностной модели на основе аксиом А.Н. Колмогорова. Ознакомиться с правилами построения алгебры борелевских множеств и типами вероятностных функций, задаваемых на измеримых пространствах.
Вероятностная функция P любому случайному событию A, являющемуся элементом алгебры A, ставит в соответствие число ![]() ,
, ![]() . Кратко это
записывается так: P:
A
. Кратко это
записывается так: P:
A![]() . Это число
. Это число ![]() называется «вероятностью
наступления случайного события A» и оно понимается как значение меры возможности наступления,
осуществления события A
при однократном проведении испытания, опыта. Чем больше это число
называется «вероятностью
наступления случайного события A» и оно понимается как значение меры возможности наступления,
осуществления события A
при однократном проведении испытания, опыта. Чем больше это число ![]() , тем больше у испытателя
уверенность в возможности наступления, осуществления события A при проведении испытания и,
наоборот, чем меньше это число
, тем больше у испытателя
уверенность в возможности наступления, осуществления события A при проведении испытания и,
наоборот, чем меньше это число ![]() , тем
меньше у него уверенность в возможности его наступления, осуществления.
, тем
меньше у него уверенность в возможности его наступления, осуществления.
Но ранее функция P вводилась посредством
предварительного, аксиоматического установления соответствия ![]() . Это соответствие всегда
можно было установить, так как в рассматриваемых моделях элементарные исходы
представлялись в виде конечной или бесконечной последовательности
. Это соответствие всегда
можно было установить, так как в рассматриваемых моделях элементарные исходы
представлялись в виде конечной или бесконечной последовательности ![]() или
или ![]() . То есть, мы могли вводить
функцию P, если множество W было конечным или счётным и мы могли
мысленно представить себе каждый элементарный исход.
. То есть, мы могли вводить
функцию P, если множество W было конечным или счётным и мы могли
мысленно представить себе каждый элементарный исход.
Но есть большое
количество примеров описания испытаний, в которых элементарные исходы нельзя
представить в виде конечной или бесконечной последовательности. Например, выбор
наудачу точки из отрезка ![]() ; определение
времени горения электрической лампы; измерение высоты растения пшеницы;
взвешивание зерен одного колоса пшеницы.
; определение
времени горения электрической лампы; измерение высоты растения пшеницы;
взвешивание зерен одного колоса пшеницы.
Такие множества, все элементы которых нельзя представить в виде конечной или бесконечной последовательности, называются множествами мощности континуум.
Сохранив основные понятия
и определения, сделанные при рассмотрении примеров, определяющих множества
конечной или счетной мощности, и расширив определение алгебры на случай
рассмотрения счетных последовательностей событий до определения s-алгебры, мы, следуя А.Н. Колмогорову,
вероятностную функцию P
определяем как числовую функцию определенную на элементах s-алгебры A. Но, если раньше нормированность и аддитивность
вероятностной функции P
вытекали автоматически из ее определения по набору положительных чисел ![]() то теперь, при построении
общей вероятностной модели, нормированность и s-аддитивность функции P требуется аксиоматически. То есть, всякая функция,
определенная на s-алгебре
случайных событий, принимающая числовые значения и обладающая свойствами
нормированности и s-аддитивности,
является вероятностной функцией.
то теперь, при построении
общей вероятностной модели, нормированность и s-аддитивность функции P требуется аксиоматически. То есть, всякая функция,
определенная на s-алгебре
случайных событий, принимающая числовые значения и обладающая свойствами
нормированности и s-аддитивности,
является вероятностной функцией.
Рассматривая свойства вероятностной функции, приходим к выводу, что вместо s-аддитивности аксиоматически можно требовать или «непрерывность сверху», или «непрерывность снизу», или «непрерывность в нуле». (Аналогично тому, как при изучении геометрии, основывающуюся на аксиомах Евклида, вместо пятой аксиомы параллельности можно принять аксиому о том, что сумма углов треугольника равна p.)
Тройку объектов <W,A,P> называется вероятностным пространством. Для того чтобы показать как практически реализуется процесс построения вероятностного пространства по Колмогорову, рассматриваются такие испытания, элементарными исходами которых будут действительные числа (или – точки вещественной оси).
Однако, если мы будем в качестве алгебры событий, то есть в качестве области определения вероятностной функции P брать s-алгебру всех подмножеств множества действительных чисел, то получится очень необозримая алгебра множеств, на которой будет невозможно задать числовую функцию. Поэтому в качестве алгебры случайных событий предлагается взять алгебру борелевских множеств. Так как мы знаем как строится, конструируется из простейших множеств полуинтервалов любое борелевское множество, то тогда, исходя из определения функции P на полуинтервалах, можно будет определить вероятностную функцию на всей s-алгебре борелевских множеств действительных чисел.
Приступая к практическому рассмотрению возможных типов и конкретных примеров вероятностных функций, в качестве множества элементарных исходов W рассматриваются множества двух типов.
I тип. W - множества вещественных чисел,
имеющие не более чем счетную мощность и лебегову меру равную нулю, то есть çWç= n или a
и ![]() (W)=0.
(W)=0.
II тип. W - множества вещественных чисел,
имеющие мощность континуум и положительную лебегову меру, то есть çWç= c и ![]() (W)>0.
(W)>0.
Соответственно этим двум типам множеств элементарных исходов определяются два типа вероятностных функций.
Функция P называется вероятностной функцией дискретного
типа, если область её определения есть множество первого типа, а множеством
ее возможных значений является не более чем счетное множество положительных
чисел ![]() таких что
таких что ![]() .
.
Функция P называется вероятностной функцией непрерывного
типа, если областью её определения является множество второго типа.
Задаётся такая функция с помощью определения кусочно-непрерывной
неотрицательной функции ![]() ,
называемой плотностью вероятностей, такой что
,
называемой плотностью вероятностей, такой что ![]()
Вероятность любого
случайного события A,
являющегося элементом алгебры B(![]() ), в зависимости от типа функции P определяется так:
), в зависимости от типа функции P определяется так:
![]() или
или ![]() .
.
Модуль 3. Случайные величины и векторы
Цель модуля: На основе понятия функции, как правиле отображения одного множества в другое, ознакомиться с понятием случайной величины. Понять универсальность использования случайной величины в решении различных практических задач. Изучить типы случайных величин и наиболее часто встречающиеся на практике законы распределения вероятностей.
Решая конкретную задачу по теории вероятностей, мы, прежде всего, определяем чёткое название элементарного исхода. Все возможные элементарные исходы объединяются во множество элементарных исходов W. Формулируя названия различных подмножеств множества элементарных исходов, определяем алгебру случайных событий A. На измеримом пространстве <W,A,> Разумным способом определяем вероятностную функцию P. То есть, при решении задачи строится вероятностное пространство <W,A, P >. Значения вероятностной функции на каждом случайном событии мы трактуем как вероятность наступления этого случайного события.
Элементарными исходами, образующими множество W, могут быть объекты любой природы:
наборы шаров различных цветов, наборы деталей различного качества, наборы карт
различных номиналов, полученные каким-либо способом, определяемым условием
испытания; последовательности событий A и ![]() ,
наступающих при проведении одинаковых испытаний по какому-либо правилу.
Введение понятия случайной величины позволяет каждому элементарному исходу,
независимо от его природы/ поставить в соответствие некоторый элемент (точку)
из пространства
,
наступающих при проведении одинаковых испытаний по какому-либо правилу.
Введение понятия случайной величины позволяет каждому элементарному исходу,
независимо от его природы/ поставить в соответствие некоторый элемент (точку)
из пространства ![]() .
.
Случайная величина ![]() – это измеримое
отображение множества элементарных исходов W в пространство
– это измеримое
отображение множества элементарных исходов W в пространство ![]() , то есть
, то есть ![]() .
Измеримость отображения означает, что для любого борелевского множества B,
.
Измеримость отображения означает, что для любого борелевского множества B, ![]() B(
B(![]() ), вероятность
случайного события
), вероятность
случайного события ![]() равна вероятности
случайного события A,
где событие A, являющееся
элементом алгебры А
равна вероятности
случайного события A,
где событие A, являющееся
элементом алгебры А![]() A,
есть полный прообраз множества В. То есть,
A,
есть полный прообраз множества В. То есть, ![]() ,
где
,
где ![]() .
.
В соответствии с типом вероятностной функции P, описывающей распределение
вероятностей значений случайной величины ![]() ,
рассматриваются два типа случайных величин: дискретный и непрерывный.
,
рассматриваются два типа случайных величин: дискретный и непрерывный.
Для любого испытания, определяющего элементарные исходы как
объекты некоторой природы (наборы карт, выборки шаров, извлеченные детали и
т.п.), мы можем теперь, с помощью понятия случайной величины, случайные события
трактовать как числовые, борелевские множества в пространстве ![]() .
.
Переход к трактовке случайных событий, независимо от содержания
условия задачи, как числовых множеств точек в ![]() ,
являющихся борелевскими множествами, позволяет ввести определение функции
распределения случайной величины.
,
являющихся борелевскими множествами, позволяет ввести определение функции
распределения случайной величины.
Для любой точки ![]() пространства
пространства ![]() множество,
точек принадлежащих интервалу
множество,
точек принадлежащих интервалу ![]() ,
обозначим
,
обозначим ![]() Ясно, что
Ясно, что ![]() - борелевское множество. Случайное событие
- борелевское множество. Случайное событие ![]() можно трактовать так:
случайная величина
можно трактовать так:
случайная величина ![]() принимает
числовые значения меньшие, чем x, т.е.:
принимает
числовые значения меньшие, чем x, т.е.: ![]() . Для каждого x мы можем определить вероятность
события
. Для каждого x мы можем определить вероятность
события ![]() , то есть число
, то есть число![]() . Если x будет переменной величиной, то эта
вероятность будет функцией от этого x. Эту функцию, обозначим её
. Если x будет переменной величиной, то эта
вероятность будет функцией от этого x. Эту функцию, обозначим её ![]() , будем называть функцией
распределения случайной величины
, будем называть функцией
распределения случайной величины ![]() :
: ![]() .
.
Если ![]() - дискретного
типа, то её функция распределения имеет вид:
- дискретного
типа, то её функция распределения имеет вид: ![]() . Если
. Если ![]() - непрерывного типа, то е
функция распределения имеет вид:
- непрерывного типа, то е
функция распределения имеет вид: 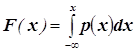 .
.
Независимо от типа случайной величины вероятность любого
случайного события B,
то есть ![]() , будет равна приращению
значения функции распределения на множестве B:
, будет равна приращению
значения функции распределения на множестве B: ![]() .
.
По любой вероятностной функции P можно построить функцию распределения ![]() . Справедливо и обратное
утверждение: всякая функция, обладающая тремя рассмотренными свойствами,
является функцией распределения
. Справедливо и обратное
утверждение: всякая функция, обладающая тремя рассмотренными свойствами,
является функцией распределения ![]() и по
ней можно единственным образом построить вероятностную функцию P.
и по
ней можно единственным образом построить вероятностную функцию P.
Рассматривая композицию отображений ![]() , приходим к понятию k-той компоненты векторной случайной
величины:
, приходим к понятию k-той компоненты векторной случайной
величины: ![]()
![]() , где
, где ![]() и к представлению
и к представлению ![]() Частная вероятностная
функция
Частная вероятностная
функция ![]() и частная функция
распределения
и частная функция
распределения ![]() каждой
каждой ![]() той компоненты
той компоненты ![]() определяется по
вероятностной функции P
и функции распределения
определяется по
вероятностной функции P
и функции распределения ![]() векторной
случайной величины
векторной
случайной величины ![]() .
.
Понятие независимости случайных величин – одно из
важнейших понятий теории вероятностей. Оно вводится как понятие независимости
компонент векторной случайной величины ![]() .
.
Компоненты ![]() называются
независимыми, если для любого множества
называются
независимыми, если для любого множества ![]() ,
принадлежащего
,
принадлежащего ![]() , вероятность
, вероятность ![]() равна произведению
вероятностей
равна произведению
вероятностей ![]() ,
, ![]() , где
, где ![]() - проекция множества
- проекция множества ![]() на
на ![]() . Рассматриваются три формы
критерия независимости случайных величин. Показывается, что по распределению
вероятностей вектора всегда можно найти распределения вероятностей его
компонент, а по распределениям вероятностей компонент не всегда можно построить
распределение вероятностей исходного вектора.
. Рассматриваются три формы
критерия независимости случайных величин. Показывается, что по распределению
вероятностей вектора всегда можно найти распределения вероятностей его
компонент, а по распределениям вероятностей компонент не всегда можно построить
распределение вероятностей исходного вектора.
Модуль 4. Числовые характеристики случайных величин и векторов
Цель модуля: На основе расширения понятия интеграла как интеграла от непрерывной функции по вероятностной мере определить понятия числовых характеристик. Показать на основе механической и геометрической интерпретации распределения вероятностной меры вероятностный смысл числовых характеристик. Научиться вычислять значения числовых характеристик и понимать их роль в изучении особенностей законов распределения случайных величин.
Использование
определения интеграла Римана-Стилтьеса от непрерывной функции 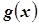 по вероятностной функции P позволяет в единой форме и независимо от типа случайной
величины
по вероятностной функции P позволяет в единой форме и независимо от типа случайной
величины 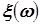 , определять:
, определять:
а) законы распределения функций случайных величин;
б) значения различных числовых характеристик случайных величин.
И в определении интеграла
Римана, и в определении интеграла Римана-Стилтьеса область Q![]() W, по которой производится
интегрирование, разбивается на отрезки
W, по которой производится
интегрирование, разбивается на отрезки ![]()
![]() В определении интеграла Римана при
составлении интегральных сумм Дарбу используется мера Лебега – длина этих
отрезков:
В определении интеграла Римана при
составлении интегральных сумм Дарбу используется мера Лебега – длина этих
отрезков: ![]() . В определении интеграла Римана-Стилтьеса при
составлении интегральных сумм, аналогичных суммам Дарбу, используется
вероятностная мера этих отрезков:
. В определении интеграла Римана-Стилтьеса при
составлении интегральных сумм, аналогичных суммам Дарбу, используется
вероятностная мера этих отрезков: ![]() . В зависимости от типа вероятностной функции P интеграл Римана-Стилтьеса есть или
сумма числового ряда, или определённый интеграл Римана.
. В зависимости от типа вероятностной функции P интеграл Римана-Стилтьеса есть или
сумма числового ряда, или определённый интеграл Римана.
Закон распределения
случайной величины, записанный в одной из его форм с помощью вероятностной
функции P или с помощью функции распределения ![]() , даёт нам всю информацию об
исследуемой случайной величине
, даёт нам всю информацию об
исследуемой случайной величине ![]() .
Числовые характеристики дают меньше информации о характере распределения
возможных значений случайной величины
.
Числовые характеристики дают меньше информации о характере распределения
возможных значений случайной величины ![]() ,
но в них аккумулированы наиболее характерные её свойства, которые позволяют нам
судить о некоторых важнейших особенностях случайной величины. Такими
характеристиками являются начальные и центральные моменты случайной величины, а
так же – функции от них.
,
но в них аккумулированы наиболее характерные её свойства, которые позволяют нам
судить о некоторых важнейших особенностях случайной величины. Такими
характеристиками являются начальные и центральные моменты случайной величины, а
так же – функции от них.
Наиболее употребительными числовыми характеристиками являются математическое ожидание – среднее значение случайной величины и дисперсия – мера рассеяния, разброса значений случайной величины около её математического ожидания.
Знание числовых значений математического ожидания и дисперсии служит задаче формулирования выводов о случайной величине и первичного представления о характере распределения е возможных значений.
При исследовании многомерной случайной величины, помимо математических ожиданий и дисперсий е компонент, рассматриваются ковариационные моменты, показывающие наличие и силу статистической связи между компонентами. Если статистические связи между компонентами имеют линейный характер, то в качестве оценки силы этой связи используется коэффициент линейной корреляции.
Функция регрессии, какого бы вида она ни была, описывает изменение значений условных математических ожиданий одной из компонент случайного вектора при изменении другой компоненты. То есть функция регрессии описывает изменение средних значений одной из случайных величин, когда другая случайная величина изменяется в области своих возможных значений.
Модуль 5. Классическая предельная проблема теории вероятностей
Цель модуля: Показать, что решение многих практических задач (в математике и механике, экономике и финансах, физике и химии, биологии и геологии и т.п.) базируется на основе знания законов распределения случайных величин, являющихся суммами большого числа независимых случайных величин – факторов. Знание результатов решения классической предельной проблемы позволит принимать план действий и делать обоснованные выводы при решении задач математической статистики.
В предельной проблеме
теории вероятностей изучаются законы распределения случайных величин,
являющиеся суммами случайных величин: ![]() ,
когда число слагаемых неограниченно возрастает
,
когда число слагаемых неограниченно возрастает ![]() .
Проблема называется классической потому, что мы рассматриваем последовательности
.
Проблема называется классической потому, что мы рассматриваем последовательности
![]() только таких случайных
величин, у которых существует конечный начальный момент второго порядка, то
есть
только таких случайных
величин, у которых существует конечный начальный момент второго порядка, то
есть ![]() .
.
Придерживаясь
исторического аспекта в изложении предельной проблемы, сначала рассматриваем
случайную величину, имеющую биномиальное распределение вероятностей ![]() .
.
1) Если проводится большое число повторных независимых испытаний (n – велико), то решение практических задач проводится путём применения локальной и интегральной теорем Муавра-Лапласа, согласно которым:
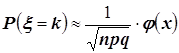 , где
, где 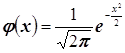 , где
, где 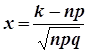 .
.
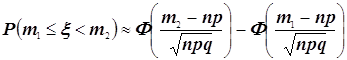 , где
, где 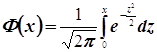 .
.
Суть этих теорем состоит
в том, что при больших значениях n биномиальное распределение вероятностей хорошо аппроксимируется
нормальным распределением N![]() . Причём
с увеличением n точность
аппроксимации возрастает.
. Причём
с увеличением n точность
аппроксимации возрастает.
То есть из интегральной
теоремы Муавра-Лапласа следует, что для функции распределения случайной
величины 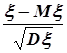 будет справедливо:
будет справедливо:
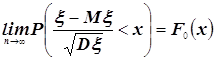 , где
, где 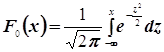 -
функция распределения нормального закона N(0,1).
-
функция распределения нормального закона N(0,1).
2) Случайная величина ![]() есть относительная частота
наступления события A при
проведении n испытаний. Теорема Бернулли
утверждает, что при неограниченном увеличении числа испытаний с вероятностью
близкой к единице, то есть практически достоверно, можно утверждать, значения
относительной частоты будут очень мало отличаться от p - вероятности наступления события A в одном испытании:
есть относительная частота
наступления события A при
проведении n испытаний. Теорема Бернулли
утверждает, что при неограниченном увеличении числа испытаний с вероятностью
близкой к единице, то есть практически достоверно, можно утверждать, значения
относительной частоты будут очень мало отличаться от p - вероятности наступления события A в одном испытании:
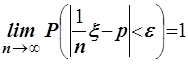 .
.
Суть этой теоремы состоит в том, что при неограниченном увеличении n относительная частота с вероятностью близкой к единице ведёт себя как постоянная величина p.
3) Если вероятность p наступления события A в одном испытании «очень мала», а
проводится большое число испытаний то, согласно теореме Пуассона, хорошую
аппроксимацию биномиального распределения вероятностей возможных значений
случайной величины![]() можно получить,
используя распределение Пуассона, то есть:
можно получить,
используя распределение Пуассона, то есть:
![]() , где
, где ![]() .
.
Случайная величина ![]() ,
,![]() , является суммой n независимых бернуллиевских случайных
величин
, является суммой n независимых бернуллиевских случайных
величин ![]() ,
, ![]() , каждая из которых есть результат
проведения одного испытания,
, каждая из которых есть результат
проведения одного испытания, ![]() . То
есть:
. То
есть: ![]() . Так как
. Так как ![]() и
и ![]() , то, заменив
, то, заменив ![]() , интегральную теорему Муавра-Лапласа
можно переписать так:
, интегральную теорему Муавра-Лапласа
можно переписать так:
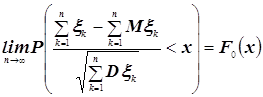 .
.
Случайную величину 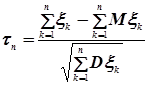 будем называть центрированной
и нормированной суммой.
будем называть центрированной
и нормированной суммой.
Интегральную теорему Муавра-Лапласа можно теперь сформулировать так:
Если ![]() , последовательность
независимых, одинаково распределённых бернуллиевских случайных величин, то, при
, последовательность
независимых, одинаково распределённых бернуллиевских случайных величин, то, при
![]() , последовательность
функций распределения случайных величин
, последовательность
функций распределения случайных величин ![]() сходится
к функции распределения нормального закона N(0,1):
сходится
к функции распределения нормального закона N(0,1):
![]() .
.
Аналогично теорему Бернулли можно, переписать так:
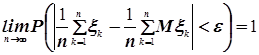 .
.
Если обозначить: ![]() , то теорему Бернулли сформулируем
так:
, то теорему Бернулли сформулируем
так:
Если ![]() , последовательность
независимых, одинаково распределённых бернуллиевских случайных величин, то, при
, последовательность
независимых, одинаково распределённых бернуллиевских случайных величин, то, при
![]() , случайная величина
, случайная величина ![]() с вероятностью близкой к
единице принимает значения, мало отличающиеся от нуля:
с вероятностью близкой к
единице принимает значения, мало отличающиеся от нуля:
![]() .
.
Обращаясь к теореме
Пуассона, рассмотрим «двойную» последовательность бернуллиевских случайных
величин ![]() . Для каждого n случайные величины
. Для каждого n случайные величины ![]() ,
, ![]() , имеют одинаковое распределение
, имеют одинаковое распределение
![]() . Вероятности
. Вероятности ![]() уменьшаются с изменением n. Обозначим
уменьшаются с изменением n. Обозначим ![]() .
.
Теорема Пуассона:
Если ![]() , но так что
, но так что ![]() , то, при
, то, при ![]() , случайная величина
, случайная величина ![]() имеет распределение
вероятностей мало отличающееся от распределения вероятностей закона Пуассона,
то есть:
имеет распределение
вероятностей мало отличающееся от распределения вероятностей закона Пуассона,
то есть:
![]() .
.
Суммируя всё, можем
сказать, что для случайной величины ![]() , являющейся
суммой независимых бернуллиевских случайных величин
, являющейся
суммой независимых бернуллиевских случайных величин ![]() ,
в качестве предельного распределения вероятностей при
,
в качестве предельного распределения вероятностей при ![]() будет нормальное,
вырожденное или пуассоновское распределение вероятностей.
будет нормальное,
вырожденное или пуассоновское распределение вероятностей.
Естественно возникает
вопрос: «А если снять ограничение, состоящее в том, что случайные величины ![]() - бернуллиевские? Какие
ограничения надо наложить на последовательность случайных величин
- бернуллиевские? Какие
ограничения надо наложить на последовательность случайных величин ![]() , чтобы их суммы
, чтобы их суммы ![]() и
и ![]() в качестве предельного при
в качестве предельного при
![]() имели, соответственно,
нормальное, вырожденное и пуассоновское распределение вероятностей?».
имели, соответственно,
нормальное, вырожденное и пуассоновское распределение вероятностей?».
Определяем три новых
понятия: «Закон больших чисел», «Центральная предельная теорема» и «Закон малых
чисел». Знакомимся с теоремами, в которых на последовательности случайных
величин ![]() налагаются ограничения,
при которых:
налагаются ограничения,
при которых:
1)![]() имеет распределение, мало
отличающееся от нормального (
имеет распределение, мало
отличающееся от нормального (![]() N(0,1));
N(0,1));
2)![]() имеет распределение, мало
отличающееся от вырожденного (
имеет распределение, мало
отличающееся от вырожденного (![]() );
);
3)![]() имеет распределение, мало
отличающееся от распределения Пуассона (
имеет распределение, мало
отличающееся от распределения Пуассона (![]() (
(![]() )).
)).
Необходимо уметь объяснить практическую значимость предельных теорем для последовательностей независимых случайных величин.
Математическая статистика
Модуль 6. Первичная обработка статистических данных. Точечные оценки числовых характеристик
Цель модуля: Узнать новую терминологию, понятия и определения математической статистики. Показать приёмы и правила первичной обработки статистических данных, принципы выбора точечных оценок числовых характеристик изучаемых случайных величин.
Математическая статистика - самостоятельная математическая дисциплина, имеющая свой словарь терминов, с которым мы знакомимся, как и при изучении теории вероятностей, путём введения основных понятий и определений. Изучение свойств введённых терминов и формулирование выводов, которые делаются по результатам обработки статистических данных, проводятся путём использования основных положений теории вероятностей.
Надо всё время иметь в виду, что все объекты и построения математической статистики являются экспериментальными моделями объектов и построений, которые вводились и изучались в теории вероятностей.
Первыми основными понятиями являются понятия «генеральная совокупность» и «выборка».
Генеральная совокупность – это все объекты, обладающие интересующим нас количественным признаком. Исследуемый количественный признак – случайная величина. Каждый объект генеральной совокупности имеет определённое значение количественного признака. Это значение количественного признака является одним из возможных значений случайной величины. Наблюдая объекты генеральной совокупности, мы фиксируем возможные значения случайной величины. Частота встречаемости возможных значений случайной величины определяется законом распределения вероятностей этой случайной величины.
Однако не всегда удаётся, а иногда просто невозможно, обследовать все объекты генеральной совокупности для определения значения количественного признака, которым они обладают. Для изучения случайной величины из генеральной совокупности отбирают некоторое количество объектов и определяют значения количественного признака, которым обладают эти объекты.
Полученные значения
количественного признака ![]() у этих
объектов будут называться статистическими данными или выборкой из
генеральной совокупности, если они репрезентативны. Под термином репрезентативность
(представительность) мы понимаем, что полученные данные вполне отражают в общих
чертах особенности количественного признака, которым обладают объекты
генеральной совокупности.
у этих
объектов будут называться статистическими данными или выборкой из
генеральной совокупности, если они репрезентативны. Под термином репрезентативность
(представительность) мы понимаем, что полученные данные вполне отражают в общих
чертах особенности количественного признака, которым обладают объекты
генеральной совокупности.
Различные методики отбора объектов из генеральной совокупности, стремятся обеспечить репрезентативность получаемых данных. Мы отмечаем, что попадание каждого объекта в выборку должно быть независимым от остальных объектов. Измерения значений количественного признака у выбранных объектов должны проводиться по одной методике, в одинаковых условиях и одним и тем же инструментом.
Если полученная выборка ![]() - репрезентативна, то на
её элементы мы будем смотреть двояко. С одной стороны мы элементы выборки будем
рассматривать как набор n
чисел, являющихся значениями эмпирической случайной величины
- репрезентативна, то на
её элементы мы будем смотреть двояко. С одной стороны мы элементы выборки будем
рассматривать как набор n
чисел, являющихся значениями эмпирической случайной величины ![]() . А с другой стороны -
как на n-мерный случайный вектор
. А с другой стороны -
как на n-мерный случайный вектор ![]() с независимыми, одинаково
распределёнными компонентами.
с независимыми, одинаково
распределёнными компонентами.
При первичной обработке
статистических данных строится вариационный ряд, являющийся, по существу,
рядом распределения эмпирической случайной величины ![]() . При этом мы считаем,
что все элементы выборки - равновозможные, то есть
. При этом мы считаем,
что все элементы выборки - равновозможные, то есть ![]() .
Геометрическая иллюстрация вариационного ряда – гистограмма даёт
наглядное представление о характере распределения вероятностей исследуемой
случайной величины
.
Геометрическая иллюстрация вариационного ряда – гистограмма даёт
наглядное представление о характере распределения вероятностей исследуемой
случайной величины ![]() . Теорема Гливенко
показывает, что при
. Теорема Гливенко
показывает, что при ![]() с вероятностью
близкой к единице значения эмпирической функции распределения
с вероятностью
близкой к единице значения эмпирической функции распределения ![]() будут очень мало отличаться
от значений теоретической функции распределения
будут очень мало отличаться
от значений теоретической функции распределения ![]() исследуемой
случайной величины
исследуемой
случайной величины ![]() .
.
Случайная величина ![]() имеет числовые
характеристики
имеет числовые
характеристики ![]() и другие.
Значения этих характеристик мы не знаем, это – теоретические числа. По
элементам выборки мы должны оценить эти теоретические числа - дать их точечные
оценки. Так как эмпирическая случайная величина
и другие.
Значения этих характеристик мы не знаем, это – теоретические числа. По
элементам выборки мы должны оценить эти теоретические числа - дать их точечные
оценки. Так как эмпирическая случайная величина ![]() понимается нами как
статистическая модель исследуемой случайной величины
понимается нами как
статистическая модель исследуемой случайной величины ![]() , то естественно принять
значения числовых характеристик
, то естественно принять
значения числовых характеристик ![]() в
качестве точечных оценок неизвестных значений числовых характеристик. Так как мы
приняли, что
в
качестве точечных оценок неизвестных значений числовых характеристик. Так как мы
приняли, что ![]() , а эмпирическая
случайная величина
, а эмпирическая
случайная величина ![]() - случайная
величина дискретного типа, то
- случайная
величина дискретного типа, то ![]() ,
, ![]() . То есть предлагается эмпирическое
математическое ожидание
. То есть предлагается эмпирическое
математическое ожидание ![]() -
среднее арифметическое элементов выборки и эмпирическую дисперсию
-
среднее арифметическое элементов выборки и эмпирическую дисперсию ![]() принять в качестве
точечных оценок.
принять в качестве
точечных оценок.
Обобщая сказанное,
теоретические числовые характеристики исследуемой случайной величины обозначим ![]() , а соответствующие
эмпирические числовые характеристики, предлагаемые в качестве оценок, обозначим
, а соответствующие
эмпирические числовые характеристики, предлагаемые в качестве оценок, обозначим
![]() .
.
Любая точечная оценка ![]() является функцией
элементов выборки:
является функцией
элементов выборки: ![]() . Элементы,
попавшие в выборку – случайные величины. Следовательно, функция
. Элементы,
попавшие в выборку – случайные величины. Следовательно, функция ![]() - случайная величина.
Всякую функцию элементов выборки будем называть статистикой.
- случайная величина.
Всякую функцию элементов выборки будем называть статистикой.
Но функций от элементов выборки можно придумать много. И каждую придуманную функцию можно предложить в качестве статистической оценки теоретической числовой характеристики. Возникает вопрос: «Как выбрать из множества предлагаемых точечных оценок наилучшую оценку?». Чтобы ответить на этот вопрос, мы должны сформулировать требования, исходящие из здравого смысла, и проверять выполнение этих требований к предлагаемым точечным оценкам. Та оценка, которая будет удовлетворять всем требованиям, будет наилучшей оценкой и будет принята в качестве точечной оценки неизвестного значения числовой характеристики.
Формулировки требований состоятельности, несмещённости и эффективности, предъявляемые к точечным оценкам, основаны на знании закона больших чисел и центральной предельной теоремы теории вероятностей. Логичность и справедливость этих требований не вызывает сомнений.
Рассматриваемые методы получения точечных оценок, позволяют обоснованным теорией вероятностей путём получать их и проверять выполнение сформулированных требований к ним.
Модуль 7. Интервальные оценки числовых характеристик
Цель модуля: Продолжить знакомство с приёмами первичной обработки статистических данных. Узнать три типа распределений случайных величин, которые используются при определении закона распределения различных функций статистических данных.
Кроме точечной оценки ![]() значения теоретической
числовой характеристики
значения теоретической
числовой характеристики ![]() изучаемой
случайной величины исследователю иногда бывает необходимо знать интервал
изучаемой
случайной величины исследователю иногда бывает необходимо знать интервал ![]() , в котором с достаточно
большой степенью уверенности
, в котором с достаточно
большой степенью уверенности ![]() (0,9;
0,95; 0,999,…) может находиться неизвестное значение числовой
характеристики
(0,9;
0,95; 0,999,…) может находиться неизвестное значение числовой
характеристики ![]() . То есть, при
заданном уровне надёжности
. То есть, при
заданном уровне надёжности ![]() ,
по имеющейся выборке
,
по имеющейся выборке ![]() надо
определить границы интервала
надо
определить границы интервала ![]() и
и ![]() так, чтобы выполнялось
неравенство:
так, чтобы выполнялось
неравенство:
![]() .
.
Вероятность ![]() называется
доверительной вероятностью, а интервал
называется
доверительной вероятностью, а интервал ![]() -
доверительным интервалом.
-
доверительным интервалом.
Ясно, что границы
интервала, как функции элементов выборки, являются статистиками – случайными
величинами: ![]() и
и ![]() . Значит для определения
при заданной доверительной вероятности их числовых значений, надо знать закон
распределения вероятностей этих статистик.
. Значит для определения
при заданной доверительной вероятности их числовых значений, надо знать закон
распределения вероятностей этих статистик.
Наиболее часто в
математической статистике используются три распределения вероятностей:
распределение Пирсона, распределение Стьюдента и распределение
Фишера-Снедекора. Случайные величины ![]() ,
, ![]() и
и ![]() , подчиняющиеся,
соответственно, этим распределениям, являются функциями независимых случайных
величин, имеющих одинаковое нормальное распределение N(0,1).
, подчиняющиеся,
соответственно, этим распределениям, являются функциями независимых случайных
величин, имеющих одинаковое нормальное распределение N(0,1).
Применение этих трёх распределений в математической статистике основано на предположении о нормальном распределении исследуемого количественного признака, определённого на генеральной совокупности, и некоторых статистик, что, в свою очередь, обосновывается центральной предельной теоремой теории вероятностей.
Модуль 8. Статистическая проверка гипотез
Цель модуля: Ознакомить студентов с одним из способов научного мышления по схеме рассуждений, называемой силлогизмом. Научить постановке задачи, практическим действиям при решении её и правилам принятия решений при статистической проверке гипотез.
Статистическая проверка гипотез осуществляется по схеме научного мышления, называемого силлогизмом.
Силлогизм – дедуктивное логическое умозаключение, состоящее из посылок и выводов.
Гипотеза – научное предположение, выдвигаемое для объяснения каких-нибудь явлений.
Исследование, изучение
количественного признака – случайной величины ![]() мы
осуществляем, наблюдая попавшие в выборку возможные значения этой случайной
величины. Проведя первичную обработку статистических данных
мы
осуществляем, наблюдая попавшие в выборку возможные значения этой случайной
величины. Проведя первичную обработку статистических данных ![]() , вычислив по этим данным
значения точечных оценок числовых характеристик, мы выдвигаем предположения - гипотезы
о виде закона распределения вероятностей, о значениях числовых характеристик
случайной величины
, вычислив по этим данным
значения точечных оценок числовых характеристик, мы выдвигаем предположения - гипотезы
о виде закона распределения вероятностей, о значениях числовых характеристик
случайной величины ![]() и т.п.
и т.п.
Гипотеза – научное предположение, выдвигаемое для объяснения каких-нибудь явлений.
Ту гипотезу, которая нам
особенно важна, или дорога, будем называть основной гипотезой и
обозначать ![]() . Остальные гипотезы (по
крайней мере, должна быть хотя бы одна гипотеза) будем называть альтернативными
гипотезами и обозначать
. Остальные гипотезы (по
крайней мере, должна быть хотя бы одна гипотеза) будем называть альтернативными
гипотезами и обозначать ![]() . На
самом деле, то есть в реальности, может быть справедлива только основная
гипотеза
. На
самом деле, то есть в реальности, может быть справедлива только основная
гипотеза ![]() , или одна из альтернативных
гипотез
, или одна из альтернативных
гипотез ![]() .
.
Для проверки
справедливости основной гипотезы ![]() подбирается
критерий проверки гипотезы
подбирается
критерий проверки гипотезы ![]() ,
являющийся мерой расхождения между предполагаемыми, гипотетическими и опытными,
полученными по выборке, значениями или характеристиками исследуемой случайной
величины. Критерий
,
являющийся мерой расхождения между предполагаемыми, гипотетическими и опытными,
полученными по выборке, значениями или характеристиками исследуемой случайной
величины. Критерий ![]() - функция
элементов выборки, статистика. Следовательно, существует закон распределения
статистики T:
- функция
элементов выборки, статистика. Следовательно, существует закон распределения
статистики T: ![]() .
.
Для проверки того, какая
из выдвинутых гипотез справедлива, проводится опыт, в результате которого
получаем выборку ![]() . Определив
значение критерия
. Определив
значение критерия ![]() , мы наблюдаем
одно из двух случайных событий
, мы наблюдаем
одно из двух случайных событий ![]() или
или ![]() . Нам известно, что если
гипотеза
. Нам известно, что если
гипотеза ![]() верна, то событие
верна, то событие ![]() наступить не может, то
есть
наступить не может, то
есть ![]() .
.
Если у нас имеет место
событие ![]() , то мы говорим, что гипотеза
, то мы говорим, что гипотеза
![]() неверна, то есть мы е
отклоняем и принимаем альтернативную гипотезу.
неверна, то есть мы е
отклоняем и принимаем альтернативную гипотезу.
Так как реально мы
всегда находимся в условиях статистически устойчивой случайности, то мы
понимаем, что при верной гипотезе ![]() событие
событие
![]() может наступить, но его
вероятность
может наступить, но его
вероятность ![]() - мала. Поэтому при
принятии решения мы говорим: «Так как событие
- мала. Поэтому при
принятии решения мы говорим: «Так как событие ![]() практически
невозможное, его вероятность
практически
невозможное, его вероятность ![]() - очень
мала, то гипотеза
- очень
мала, то гипотеза ![]() отклоняется».
То есть мы лишь изредка будем ошибаться, и вероятность нашей ошибки будет равна
отклоняется».
То есть мы лишь изредка будем ошибаться, и вероятность нашей ошибки будет равна
![]() .
.
Если мы в результате
опыта мы будем наблюдать событие ![]() , то мы
говорим: « Так как произошло событие
, то мы
говорим: « Так как произошло событие ![]() , то у
нас нет оснований отклонять гипотезу
, то у
нас нет оснований отклонять гипотезу ![]() ».
То есть гипотеза
».
То есть гипотеза ![]() - принимается.
Так «осторожно» мы говорим в этом случае потому, что наступление события
- принимается.
Так «осторожно» мы говорим в этом случае потому, что наступление события ![]() есть результат
однократного проведения опыта. Не исключено, что при повторных проведениях
опытов это событие мы больше наблюдать не будем.
есть результат
однократного проведения опыта. Не исключено, что при повторных проведениях
опытов это событие мы больше наблюдать не будем.
Так как результаты
эксперимента являются выборкой из возможных значений исследуемой случайной
величины, то нельзя считать значения критерия ![]() детерминированными.
Поэтому при принятии решений и формулировании выводов возможны ошибки двух
видов. Поэтому при выборе критерия проверки справедливости гипотез
экспериментатор стремится подобрать или построить такой критерий, при котором
вероятности этих ошибок будут по возможности минимальными. Такие критерии
строятся на основании основных положений теории вероятностей и, прежде всего,
классической предельной проблемы. Рассматриваются примеры построения критериев
проверки гипотез для некоторых наиболее распространённых задач математической
статистики.
детерминированными.
Поэтому при принятии решений и формулировании выводов возможны ошибки двух
видов. Поэтому при выборе критерия проверки справедливости гипотез
экспериментатор стремится подобрать или построить такой критерий, при котором
вероятности этих ошибок будут по возможности минимальными. Такие критерии
строятся на основании основных положений теории вероятностей и, прежде всего,
классической предельной проблемы. Рассматриваются примеры построения критериев
проверки гипотез для некоторых наиболее распространённых задач математической
статистики.
Модуль 9. Корреляционный и регрессионный анализы
Цель модуля: Научить студентов узнавать наличие статистических связей между различными случайными количественными характеристиками изучаемых объектов и явлений; оценивать силу этих статистических связей и определять функцию регрессии одной из случайных величин на другую.
В корреляционном анализе рассматриваются статистические зависимости между случайными величинами. При этом решаются две задачи. Первая – оценка силы статистической связи между случайными величинами. Вторая – определение функции, которая описывает тенденцию изменения значений одной из случайных величин при изменении значений другой случайной величины.
Если статистическая зависимость имеет линейный характер, то сила связи оценивается коэффициентом линейной корреляции. Коэффициент линейной корреляции является теоретической числовой характеристикой двумерной случайной величины. Так как при решении практических задач экспериментатор имеет в своём распоряжении только двумерную выборку возможных значений исследуемой случайной величины, то оценка силы связи осуществляется с помощью эмпирического коэффициента линейной корреляции.
Формула эмпирического коэффициента линейной корреляции получается применением метода моментов определения точечных оценок.
Для решения второй задачи
сначала вводится понятие условной случайной величины: ![]() и
и ![]() . Определяются законы
распределения вероятностей этих условных случайных величин и их условные
математические ожидания:
. Определяются законы
распределения вероятностей этих условных случайных величин и их условные
математические ожидания: ![]() и
и ![]() .
.
Условное математическое
ожидание позволяет естественно ввести определение функции регрессии – как
функции, описывающей изменение значений условного математического ожидания
одной из случайных величин при изменении значений другой случайной величины в
области её возможных значений: ![]() и
и ![]() .
.
При выбранном виде функции регрессии вторая задача корреляционного анализа сводится к определению коэффициентов этой функции. Сначала, применяя метод наименьших квадратов, определяем статистические оценки коэффициентов функции регрессии. Коэффициенты функции регрессии, являясь статистиками, выражаются через точечные оценки числовых характеристик двумерной случайной величины. Применяя метод моментов «наоборот», записываем теоретическое уравнение функции регрессии одной случайной величины на другую.
В регрессионном анализе определяется функция регрессии случайной величины на изменение детерминированного параметра. В качестве примера рассматривается «Задача Путина В.В.» об удвоении в течение десяти лет внутреннего валового продукта Российской Федерации.
Определение остаточной дисперсии, с одной стороны, «служит» задачам корреляционного анализа, а с другой стороны, «закладывает фундамент» для решения задач методами дисперсионного анализа.
V. Экзаменационные вопросы
В каждом экзаменационном билете содержатся названия терминов и понятий теории вероятностей, которым надо дать определения, и два теоретических вопроса. Первый вопрос билета призван проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях.
1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами.
2. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: повторные независимые испытания.
3. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания до первого положительного исхода.
4. Условная вероятность. Вероятность произведения событий. Зависимые и независимые события.
5. Формула полной вероятности.
6. Формула Байеса.
7. Аксиоматическое построение вероятностной модели. Аксиомы А.Н. Колмогорова.
8. Свойства ![]() вероятностной
функции.
вероятностной
функции.
9. Теорема о непрерывности вероятностной
функции. Импликации ![]() и
и ![]() .
.
10. Теорема о непрерывности вероятностной
функции. Импликации ![]() и
и ![]() .
.
11. Измеримое пространство <R,B(R)>. Борелевские множества на множестве вещественных чисел.
12. Измеримое пространство <Rn,B(Rn)>. Борелевские множества на плоскости.
13. Вероятностная функция дискретного типа на измеримых пространствах <R,B(R)> и <Rn,B(Rn)>. Примеры.
14. Вероятностная функция непрерывного типа на измеримых пространствах <R,B(R)> и <Rn,B(Rn)>. Примеры.
15. Случайная величина. Типы случайных величин. Функция распределения случайной величины.
16. Случайный вектор. Компоненты случайного вектора. Частные вероятностные функции и частные функции распределения.
17. Функция распределения. Свойства. Примеры функций распределения дискретного типа.
18. Функция распределения. Свойства. Примеры функций распределения непрерывного типа.
19. Многомерная функция распределения. Свойства. Примеры. Свойства согласованности.
20. Независимость компонент случайного вектора. Критерий независимости.
21. Математическое ожидание случайной величины. Определение. Примеры.
22. Математическое ожидание случайной величины. Определение. Свойства.
23. Дисперсия случайной величины. Определение. Примеры.
24. Дисперсия случайной величины. Определение. Свойства.
25. Функции случайных величин. Определение закона распределения функции случайной величины. Примеры.
26. Функция распределения суммы двух независимых случайных величин. Свёртка функций распределения.
27. Начальные и центральные моменты случайной величины.
28. Числовые характеристики случайного вектора. Ковариационный момент. Ковариационная матрица.
29. Коэффициент линейной корреляции. Определение. Свойства.
30. Характеристические функции. Определение Примеры.
31. Характеристические функции. Свойства ![]() .
.
32. Характеристические функции. Свойства ![]() .
.
33. Закон больших чисел. Теорема Бернулли и теорема А.Я. Хинчина. Правило среднего арифметического.
34. Закон больших чисел. Неравенство и теорема П.Л. Чебышёва.
35. Центральная предельная теорема. Теорема Муавра-Лапласа.
36. Центральная предельная теорема. Теорема Леви. Следствия.
37. Центральная предельная теорема. Понятия о теоремах А.М. Ляпунова и Линдебега-Феллера.
38. Закон малых чисел. Теорема Пуассона.
39. Выборка. Первичная обработка статистических данных. Теорема Гливенко.
40. Точечные оценки числовых характеристик случайных величин. Требования к точечным оценкам.
41. Неравенство Рао-Крамера. Эффективность оценки математического ожидания - среднего арифметического элементов выборки.
42. Метод моментов получения точечных оценок числовых характеристик случайных величин.
43. Метод максимального правдоподобия получения точечных оценок числовых характеристик случайных величин.
44. Некоторые специальные распределения, используемые в математической статистике.
45. Интервальные оценки числовых характеристик случайных величин. Доверительный интервал для математического ожидания.
46. Интервальные оценки числовых характеристик случайных величин. Доверительный интервал для дисперсии.
47. Статистическая проверка гипотез. Ошибки первого и второго рода. Три типа задач статистической проверки гипотез.
48. Статистическая проверка гипотезы о равенстве математического ожидания некоторому фиксированному числу.
49. Статистическая проверка гипотезы о равенстве дисперсии некоторому фиксированному числу.
50. Статистическая проверка гипотезы о равенстве дисперсий двух различных случайных величин.
51. Статистическая проверка гипотезы о равенстве математических ожиданий двух различных случайных величин.
52. Статистическая проверка гипотез. Понятия о критериях Колмогорова и Мизеса.
53. Статистическая проверка гипотезы о виде закона распределения случайной величины. Критерий согласия Пирсона.
54. Элементы корреляционного и дисперсионного анализов. Две задачи корреляционного анализа. Статистическая оценка коэффициента линейной корреляции.
55. Условные распределения и условные математические ожидания. Определение функции регрессии.
56. Статистическая оценка коэффициентов линейной функции регрессии методом наименьших квадратов.
57. Остаточная дисперсия при линейной регрессии.
58. Корреляционное отношение – мера силы статистической связи при нелинейной регрессии.
Образцы вариантов контрольных работ по теории вероятностей
Контрольная работа №1
ВАРИАНТ образец
1. На девяти карточках написаны цифры 1,2,3,4,5,6,7,8,9. Из них наудачу выбираются две карточки и кладутся на стол в порядке появления. Найти вероятность того, что полученное число делится на семь.
2. Имеются три станка. Каждый из них может работать в данный момент с вероятностью 0,7, 0,8 и 0,9 соответственно. Найти вероятность того, что в данный момент будут работать только два станка.
3. В первой урне имеются три белых и семь чёрных шаров, а во второй – семь белых и три чёрных шара. Из первой урны во вторую наудачу переложен шар, а затем, также наудачу, переложен шар из второй урны в первую. Определить вероятность того, что составы урн после этих перекладываний не изменятся.
4. Станок автомат, выпускающий детали, даёт 5% брака. Существующая система контроля качества 90% процентов бракованных деталей называет бракованными, но, в силу своего несовершенства, 5% доброкачественных деталей объявляет бракованными. Деталь, прошедшая контроль, названа бракованной. Какова вероятность того, что контроль не ошибся?
ВАРИАНТ № образец
1. В урне шесть белых и четыре чёрных шара. Из урны вынимают наудачу пять шаров. Найти вероятность того, что два из них будут белыми, а три – чёрными.
2. В первой партии 45 годных и 5 бракованных деталей, во второй партии 50 годных и 10 бракованных деталей. Наудачу из каждой партии берут по одной детали. Найти вероятность того, что они обе бракованные.
3. Наугад выбираются по одной букве из слов «корова» и «кошка». Найти вероятность того, что эти буквы окажутся одинаковыми.
4. Брошено две монеты. Если выпали два «герба», то из урны №1 извлекается один шар, в противном случае шар извлекается из урны №2. Урна №1 содержит пять чёрных и два белых шара. Урна №2 содержит два чёрных и пять белых шаров. Какова вероятность того, что шар извлекался из урны 1, если он оказался чёрным?
ВАРИАНТ № образец
1. Игральная кость бросается два раза. Найти вероятность того, что во второй раз выпадет большее число очков, чем в первый раз.
2. В первой урне 10 белых и 15 чёрных шаров, во второй урне 12 белых и 20 чёрных шаров и в третьей 15 белых и 10 чёрных шаров. Из каждой урны наудачу извлекают по два шара. Найти вероятность того, что все вынутые шары одного цвета.
3. Пассажир забыл последнюю цифру шифра в автоматической камере хранения и набирает её наудачу. Определить вероятность того, что для открытия ячейки ему понадобится не более четырёх попыток.
4. В левом кармане пять монет по 50 коп. и три монеты по 10 коп., а в правом кармане четыре монеты по 50 коп. и шесть монет по 10 коп. Из правого кармана в левый наудачу перекладывается одна монета, после чего из левого кармана также наудачу извлекается одна монета, оказавшаяся пятидесятикопеечной. Какова вероятность того, что в левый карман была переложена десятикопеечная монета?
Контрольная работа №2
ВАРИАНТ № образец
1. Из колоды карт (52 шт.) наудачу без возвращения извлекаются восемь карт. Постройте ряд распределения и определите мат. ожидание случайного числа появившихся красных картинок. Чему равна вероятность того, что число этих картинок - чётное?
2. При каком значении параметра а функция:
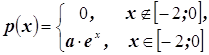
будет плотностью
вероятности случайной величины x. Найти функцию распределения F(x), математическое ожидание Мx. Чему равна вероятность случайного
события ![]() ? Сделать чертёж.
? Сделать чертёж.
ВАРИАНТ № образец
1. Две игральных кости одновременно подбрасывают шесть раз. Постройте ряд распределения случайного числа появлений хотя бы одной шестёрки на верхних гранях брошенных костей. Чему равно мат. ожидание этого случайного числа?
2. При каком значении параметра а функция:
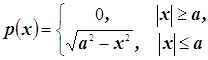
будет плотностью
вероятности случайной величины x. Найти математическое ожидание Мx. Чему равна вероятность случайного
события 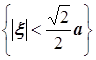 ? Сделать чертёж.
? Сделать чертёж.
ВАРИАНТ № образец
1. Баскетболист бросает мяч в корзину до
первого попадания, но ему разрешается сделать не более пяти попыток. Постройте
ряд распределения случайного числа сделанных промахов. Чему равна вероятность
того, что число сделанных промахов будет нечётным, если вероятность попадания
при одном броске у этого баскетболиста равна ![]() ?
?
2. При каком значении параметра а функция:
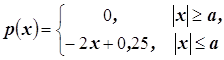
будет плотностью
вероятности случайной величины x. Найти функцию распределения F(x), математическое ожидание Мx. Чему равна вероятность случайного
события ![]() ? Сделать чертёж.
? Сделать чертёж.
Контрольная работа №3
ВАРИАНТ № образец
1. На одной из сторон правильного треугольника, длина стороны которого равна а, наудачу ставится точка. Через эту точку, параллельно двум другим сторонам треугольника, проводятся две прямые. Определите математическое ожидание и дисперсию величины площади получившегося параллелограмма.
2. В урне находятся один белый, два красных и три чёрных шара. Наудачу без возвращения извлекаются три шара. Для случайных чисел появившихся шаров белого и красного цвета постройте таблицу распределения вероятностей. Найти частные распределения компонент получившегося вектора.
3.
Случайная
величина ![]() является средней
арифметической 3600 независимых одинаково распределённых случайных величин, у
каждой из которых математическое ожидание равно трём, а дисперсия – двум. Каким
должно быть
является средней
арифметической 3600 независимых одинаково распределённых случайных величин, у
каждой из которых математическое ожидание равно трём, а дисперсия – двум. Каким
должно быть ![]() , чтобы суверенностью не
менее, чем 0,95 можно было утверждать, что значения
, чтобы суверенностью не
менее, чем 0,95 можно было утверждать, что значения ![]() отклонятся
от
отклонятся
от ![]() меньше, чем на
меньше, чем на ![]() ?
?
ВАРИАНТ № образец
1. На окружности радиуса r наудачу ставится точка. Из этой точки параллельно горизонтальному и вертикальному диаметрам проводятся две хорды, которые берутся в качестве сторон прямоугольника. Две другие стороны прямоугольника, проводятся параллельно этим хордам. Определите математическое ожидание и дисперсию величины площади получающегося прямоугольника.
2. В первой урне находятся два белых и три чёрных шара. Во второй урне – три белых и два чёрных шара. Из первой урны во вторую наудачу перекладывается один шар, а затем из второй урны сразу извлекаются два шара. Для двумерной случайной величины – число переложенных и число извлечённых шаров белого цвета построить таблицу распределения. Найти частные распределения компонент.
3.
С
какой уверенностью можно ожидать, что при 900 подбрасываниях игральной кости
значение относительной частоты выпадений нечётного числа очков отклонится от вероятности
![]() менее чем на 0,015?
менее чем на 0,015?
ВАРИАНТ № образец
1. По сторонам прямого угла образованного координатными осями, концами скользит линейка длиною l. Все значения координаты её правого конца на оси абсцисс – равновозможные. Найдите математическое ожидание величины расстояния от линейки до начала координат.
2. В урне находятся один белый, два красных и три чёрных шара. Наудачу с возвращением каждый раз извлекаются два шара. Для случайных чисел появившихся шаров белого и красного цвета постройте таблицу распределения вероятностей.
3. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с уверенностью не меньшей чем 0,95 можно было утверждать, что число наступлений события будет не менее 80?
VI. Индивидуальные задания по математической статистике
Методические указания
Для лучшего усвоения приёмов и методов математической статистики каждый студент получает индивидуальное задание.
Это задание представляет собой наборы статистических данных, полученных экспериментальным путём, и являются выборками значений двумерных случайных величин. В ходе выполнения работы студент должен выполнить следующие пять заданий, соответствующим пяти модулям теоретического курса.
1. Первичная обработка статистических данных.
Необходимо построить вариационные ряды. Построить гистограммы. Определить значения точечных оценок числовых характеристик случайных величин.
2. Интервальные оценки числовых характеристик случайных величин.
Построение доверительных интервалов для математических ожиданий и дисперсий. Приобретение навыков работы с таблицами специальных распределений математической статистики.
3. Статистическая проверка гипотез.
Решаются три задачи. Проверка гипотез о равенстве значений числовых характеристик некоторому фиксированному числу. Проверка гипотез о совпадении значений одноимённых числовых характеристик двух случайных величин.
4. Проверка гипотезы о виде закона распределения исследуемой случайной величины.
Критерий «согласия» Пирсона. Проверка гипотезы о совпадении законов распределения двух случайных величин.
5. Корреляционный анализ.
Оценка силы статистической связи между случайными величинами. Определение методом наименьших квадратов статистических оценок коэффициентов функции регрессии. Построение соответствующей геометрической иллюстрации.
Все задания выполняются последовательно по мере накопления теоретического материала. Студент представляет для зачёта каждое выполненное задание. Выполнение заданий предполагает использование персонального компьютера. Все задания представляются в распечатанном виде. После получения зачёта выполненные задания остаются у студента и могут в дальнейшем быть использованы как руководства по математической обработке статистических материалов.
Образцы статистических данных для выполнения индивидуальных заданий
Вариант № образец
Двумерная случайная величина дискретного типа
Длина слова (выборки ![]() и
и ![]() ) и количество гласных в
этом слове (выборки
) и количество гласных в
этом слове (выборки ![]() и
и ![]() ) в орфографическом словаре
русского языка.
) в орфографическом словаре
русского языка.
| № |
|
|
|
|
№ |
|
|
|
|
| 1 | 6 | 3 | 4 | 2 | 51 | 9 | 3 | 7 | 3 |
| 2 | 16 | 7 | 7 | 3 | 52 | 8 | 3 | 8 | 3 |
| 3 | 4 | 2 | 9 | 4 | 53 | 9 | 3 | 6 | 2 |
| 4 | 8 | 4 | 7 | 3 | 54 | 9 | 3 | 8 | 4 |
| 5 | 5 | 2 | 6 | 2 | 55 | 11 | 5 | 7 | 2 |
| 6 | 9 | 3 | 6 | 2 | 56 | 15 | 7 | 8 | 2 |
| 7 | 12 | 6 | 7 | 3 | 57 | 8 | 2 | 3 | 1 |
| 8 | 11 | 6 | 8 | 3 | 58 | 10 | 4 | 7 | 3 |
| 9 | 9 | 5 | 6 | 3 | 59 | 6 | 2 | 9 | 4 |
| 10 | 7 | 3 | 5 | 3 | 60 | 7 | 2 | 7 | 3 |
| 11 | 8 | 3 | 7 | 3 | 61 | 8 | 3 | 7 | 3 |
| 12 | 8 | 4 | 7 | 3 | 62 | 6 | 4 | 11 | 5 |
| 13 | 6 | 3 | 5 | 2 | 63 | 5 | 2 | 9 | 4 |
| 14 | 9 | 5 | 8 | 3 | 64 | 7 | 3 | 7 | 3 |
| 15 | 5 | 2 | 5 | 2 | 65 | 5 | 2 | 7 | 3 |
| 16 | 7 | 4 | 12 | 4 | 66 | 5 | 2 | 6 | 2 |
| 17 | 10 | 6 | 5 | 2 | 67 | 7 | 2 | 8 | 3 |
| 18 | 9 | 4 | 5 | 2 | 68 | 9 | 5 | 8 | 3 |
| 19 | 10 | 5 | 8 | 3 | 69 | 7 | 3 | 9 | 5 |
| 20 | 14 | 7 | 9 | 3 | 70 | 5 | 2 | 6 | 3 |
| 21 | 12 | 5 | 5 | 2 | 71 | 8 | 3 | 7 | 3 |
| 22 | 7 | 3 | 7 | 3 | 72 | 7 | 3 | 6 | 2 |
| 23 | 7 | 3 | 5 | 2 | 73 | 10 | 5 | 5 | 2 |
| 24 | 6 | 3 | 3 | 1 | 74 | 8 | 4 | 8 | 3 |
| 25 | 7 | 4 | 4 | 2 | 75 | 8 | 3 | 8 | 4 |
| 26 | 12 | 6 | 7 | 2 | 76 | 8 | 3 | 5 | 2 |
| 27 | 12 | 6 | 8 | 3 | 77 | 5 | 2 | 12 | 4 |
| 28 | 8 | 5 | 5 | 2 | 78 | 12 | 5 | 11 | 6 |
| 29 | 9 | 4 | 7 | 3 | 79 | 15 | 6 | 5 | 2 |
| 30 | 7 | 3 | 5 | 2 | 80 | 9 | 4 | 6 | 2 |
| 31 | 12 | 7 | 3 | 1 | 81 | 7 | 3 | 4 | 1 |
| 32 | 7 | 3 | 6 | 2 | 82 | 8 | 4 | 7 | 3 |
| 33 | 8 | 4 | 6 | 2 | 83 | 10 | 4 | 7 | 2 |
| 34 | 5 | 2 | 7 | 3 | 84 | 4 | 2 | 10 | 4 |
| 35 | 8 | 3 | 8 | 3 | 85 | 9 | 4 | 6 | 2 |
| 36 | 7 | 4 | 5 | 2 | 86 | 6 | 4 | 14 | 7 |
| 37 | 11 | 5 | 8 | 3 | 87 | 5 | 2 | 12 | 5 |
| 38 | 6 | 3 | 6 | 2 | 88 | 5 | 2 | 8 | 3 |
| 39 | 5 | 2 | 6 | 2 | 89 | 6 | 2 | 8 | 3 |
| 40 | 7 | 3 | 9 | 3 | 90 | 10 | 4 | 5 | 2 |
| 41 | 9 | 4 | 7 | 2 | 91 | 5 | 3 | 7 | 3 |
| 42 | 5 | 2 | 3 | 1 | 92 | 8 | 5 | 5 | 2 |
| 43 | 6 | 2 | 8 | 3 | 93 | 17 | 8 | 6 | 2 |
| 44 | 10 | 4 | 10 | 4 | 94 | 18 | 7 | 15 | 7 |
| 45 | 10 | 4 | 7 | 4 | 95 | 7 | 5 | 10 | 4 |
| 46 | 7 | 3 | 5 | 2 | 96 | 7 | 4 | 10 | 4 |
| 47 | 17 | 9 | 7 | 4 | 97 | 5 | 3 | 8 | 4 |
| 48 | 10 | 4 | 5 | 2 | 98 | 6 | 3 | 6 | 3 |
| 49 | 10 | 4 | 10 | 4 | 99 | 10 | 5 | 6 | 2 |
| 50 | 9 | 5 | 7 | 3 | 100 | 7 | 4 | 11 | 3 |
Вариант № образец
Двумерная случайная величина непрерывного типа
Рост (см) (выборки ![]() и
и ![]() ) и Длина окружности
грудной клетки (см) (выборки
) и Длина окружности
грудной клетки (см) (выборки ![]() и
и ![]() ) двух групп обследованных
юношей-призывников.
) двух групп обследованных
юношей-призывников.
| № |
|
|
|
|
№ |
|
|
|
|
| 1 | 157,5 | 84,0 | 159,5 | 85,0 | 51 | 162,5 | 87,5 | 170,0 | 88,5 |
| 2 | 165,0 | 89,5 | 169,5 | 88,0 | 52 | 168,0 | 86,5 | 161,5 | 87,5 |
| 3 | 160,0 | 82,5 | 155,5 | 81,5 | 53 | 157,0 | 80,5 | 166,5 | 88,0 |
| 4 | 164,0 | 85,0 | 164,5 | 88,5 | 54 | 163,5 | 90,0 | 154,0 | 80,0 |
| 5 | 162,0 | 84,5 | 173,0 | 83,5 | 55 | 160,5 | 87,0 | 168,5 | 83,0 |
| 6 | 165,5 | 85,0 | 158,5 | 86,5 | 56 | 169,5 | 86,5 | 162,5 | 89,0 |
| 7 | 169,5 | 87,0 | 173,5 | 91,5 | 57 | 166,5 | 84,0 | 165,0 | 86,0 |
| 8 | 155,5 | 78,0 | 165,5 | 81,5 | 58 | 164,0 | 87,0 | 160,0 | 84,0 |
| 9 | 172,5 | 83,5 | 161,5 | 78,0 | 59 | 175,0 | 83,5 | 177,0 | 90,0 |
| 10 | 163,0 | 83,0 | 166,5 | 89,5 | 60 | 158,0 | 84,5 | 164,0 | 87,5 |
| 11 | 158,5 | 83,0 | 152,0 | 81,5 | 61 | 162,0 | 88,0 | 174,5 | 90,0 |
| 12 | 166,0 | 90,0 | 166,0 | 87,0 | 62 | 158,5 | 89,5 | 158,5 | 81,5 |
| 13 | 168,5 | 91,5 | 163,0 | 84,5 | 63 | 174,5 | 88,5 | 166,0 | 90,0 |
| 14 | 161,0 | 80,0 | 167,0 | 86,5 | 64 | 166,5 | 88,0 | 167,0 | 88,5 |
| 15 | 167,0 | 84,5 | 157,5 | 79,5 | 65 | 163,0 | 86,0 | 160,0 | 81,5 |
| 16 | 153,0 | 79,5 | 167,5 | 81,0 | 66 | 165,5 | 83,5 | 168,5 | 85,5 |
| 17 | 164,5 | 79,0 | 162,0 | 79,5 | 67 | 170,5 | 86,0 | 162,5 | 83,5 |
| 18 | 165,5 | 88,5 | 164,5 | 79,0 | 68 | 160,0 | 86,0 | 163,5 | 91,5 |
| 19 | 160,0 | 88,0 | 169,0 | 87,0 | 69 | 163,5 | 80,5 | 167,5 | 85,0 |
| 20 | 167,5 | 79,5 | 160,5 | 81,0 | 70 | 176,5 | 87,5 | 157,0 | 85,5 |
| 21 | 162,5 | 79,0 | 170,5 | 81,5 | 71 | 154,5 | 85,0 | 172,5 | 92,0 |
| 22 | 171,0 | 85,5 | 162,5 | 85,0 | 72 | 172,0 | 91,5 | 164,5 | 88,0 |
| 23 | 158,0 | 77,5 | 164,0 | 93,0 | 73 | 162,5 | 83,5 | 160,0 | 90,0 |
| 24 | 168,0 | 89,0 | 171,5 | 85,0 | 74 | 169,0 | 85,5 | 175,0 | 89,5 |
| 25 | 163,5 | 84,5 | 153,5 | 79,5 | 75 | 156,5 | 82,0 | 166,0 | 86,0 |
| 26 | 170,0 | 91,0 | 170,5 | 91,0 | 76 | 164,0 | 86,0 | 161,0 | 86,0 |
| 27 | 161,0 | 80,5 | 165,5 | 83,5 | 77 | 168,0 | 85,0 | 170,5 | 83,5 |
| 28 | 172,5 | 89,5 | 163,0 | 83,5 | 78 | 159,5 | 84,5 | 162,5 | 82,5 |
| 29 | 162,0 | 85,0 | 163,0 | 84,0 | 79 | 165,0 | 81,5 | 174,5 | 87,5 |
| 30 | 164,0 | 91,5 | 166,5 | 91,5 | 80 | 171,0 | 83,5 | 161,0 | 86,5 |
| 31 | 156,0 | 78,5 | 158,0 | 83,0 | 81 | 161,0 | 79,5 | 167,5 | 84,5 |
| 32 | 165,0 | 86,5 | 165,0 | 86,5 | 82 | 174,0 | 87,0 | 165,0 | 81,0 |
| 33 | 169,0 | 93,5 | 168,0 | 90,0 | 83 | 158,5 | 87,5 | 153,0 | 83,5 |
| 34 | 160,0 | 83,0 | 169,5 | 84,5 | 84 | 166,0 | 81,5 | 169,0 | 93,5 |
| 35 | 164,5 | 77,5 | 164,5 | 89,0 | 85 | 169,5 | 87,0 | 163,5 | 89,5 |
| 36 | 173,0 | 85,5 | 169,0 | 81,5 | 86 | 162,5 | 89,5 | 162,0 | 80,0 |
| 37 | 154,0 | 79,5 | 156,0 | 82,0 | 87 | 172,5 | 86,5 | 161,0 | 82,0 |
| 38 | 167,0 | 87,5 | 167,0 | 84,0 | 88 | 152,0 | 84,0 | 167,0 | 85,0 |
| 39 | 161,5 | 80,5 | 163,5 | 87 | 89 | 168,5 | 83,0 | 171,0 | 85,5 |
| 40 | 168,5 | 81,5 | 169,5 | 90,5 | 90 | 160,5 | 83,5 | 156,5 | 83,5 |
| 41 | 165,5 | 79,5 | 157,5 | 86,5 | 91 | 157,5 | 80,0 | 164,5 | 81,5 |
| 42 | 169,0 | 80,5 | 171,0 | 89,0 | 92 | 170,5 | 87,5 | 169,0 | 86,5 |
| 43 | 166,0 | 85,5 | 161,5 | 80,5 | 93 | 162,0 | 84,0 | 159,5 | 82,5 |
| 44 | 170,0 | 79,5 | 173,0 | 85,5 | 94 | 165,0 | 91,0 | 168,0 | 83,5 |
| 45 | 163,0 | 82,5 | 165,5 | 87,5 | 95 | 157,0 | 84,5 | 166,0 | 89,0 |
| 46 | 166,5 | 81,5 | 156,5 | 87,0 | 96 | 163,5 | 83,0 | 156,0 | 85,0 |
| 47 | 150,0 | 83,0 | 172,0 | 87,0 | 97 | 167,5 | 90,0 | 166,5 | 93,5 |
| 48 | 167,5 | 84,5 | 162,5 | 86,5 | 98 | 160,0 | 81,0 | 168,0 | 87,5 |
| 49 | 159,5 | 89,5 | 174,0 | 85,5 | 99 | 167,0 | 86,5 | 160,5 | 88,0 |
| 50 | 171,5 | 89,5 | 159,0 | 83,5 | 100 | 164,0 | 87,5 | 168,5 | 87,0 |
VII. ГЛОССАРИЙ
А
Аддитивная функция – функция ![]() множеств-
элементов алгебры A, для которой из условия
множеств-
элементов алгебры A, для которой из условия ![]() ø следует, что
ø следует, что ![]() .
.
Алгебра множеств – система подмножеств A множества W, элементы которой удовлетворяют следующим требованиям:
а) ![]() A; б) для любых A и B, принадлежащих A, следует, что
A; б) для любых A и B, принадлежащих A, следует, что ![]() A и
A и ![]() A; в) если
A; в) если ![]() A, то
A, то ![]() A.
A.
Б
Борелевская алгебра
множеств B(![]() ) – система подмножеств
множества действительных чисел R, получающаяся путём применения операций объединения, пересечения и
дополнения к элементам системы
) – система подмножеств
множества действительных чисел R, получающаяся путём применения операций объединения, пересечения и
дополнения к элементам системы ![]() , где a и b – произвольные действительные числа.
, где a и b – произвольные действительные числа.
В
Вероятностное пространство <W,A, P> - тройка объектов, где
W - множество элементарных исходов;
A - ![]() -алгебра случайных событий;
-алгебра случайных событий;
P – вероятностная функция.
Д
Дискретная
случайная
величина
случайная величина, областью возможных значений которой
является не более чем счётное множество D действительных чисел 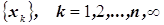 .
Закон распределения вероятностей дискретной случайной величины задаётся путём
определения набора положительных чисел
.
Закон распределения вероятностей дискретной случайной величины задаётся путём
определения набора положительных чисел 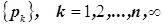 ,
таких, что
,
таких, что 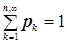 . Здесь:
. Здесь: 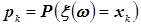 .
.
Дисперсия случайной
величины![]() - мера разброса значений случайной
величины около её математического ожидания.
- мера разброса значений случайной
величины около её математического ожидания.
Доверительный интервал
![]() - интервал, в котором с вероятностью,
не меньшей чем
- интервал, в котором с вероятностью,
не меньшей чем ![]() , находится
значение неизвестной числовой характеристики
, находится
значение неизвестной числовой характеристики ![]() ,
то есть интервал, для которого справедливо:
,
то есть интервал, для которого справедливо: ![]() .
.
З
Закон больших чисел
(ЗБЧ) – совокупность
теорем, в которых на последовательность случайных величин ![]() , налагаются условия, при
которых их среднее арифметическое
, налагаются условия, при
которых их среднее арифметическое ![]() сходится
по вероятности к постоянной величине – среднему арифметическому их
математических ожиданий:
сходится
по вероятности к постоянной величине – среднему арифметическому их
математических ожиданий: 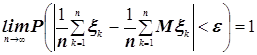 .
.
И
Измеримое пространство
<W,A> - пара объектов, где W - множество элементарных исходов,
A - алгебра случайных событий, на которой
вводится числовая функция множеств ![]() ,
которая при выполнении условий нормированности и аддитивности, называется
вероятностной мерой множества A.
,
которая при выполнении условий нормированности и аддитивности, называется
вероятностной мерой множества A.
К
Классическое
определение вероятности – определение вероятности наступления случайного события, основанное на
равновозможности реализации элементарных исходов конечного множества
элементарных исходов W.
Если мощность множества W равна
![]() , а мощность подмножества A, являющегося случайным событием,
равна
, а мощность подмножества A, являющегося случайным событием,
равна ![]() , то по классическому определению
вероятности вероятность наступления случайного события A будет равна
, то по классическому определению
вероятности вероятность наступления случайного события A будет равна ![]() .
.
Ковариационный момент – смешанный центральный момент
второго порядка ![]() двумерной
случайной величины:
двумерной
случайной величины:
![]() .
.
Компонента случайного
вектора – скалярная
случайная величина ![]() , являющаяся
проекцией случайного вектора
, являющаяся
проекцией случайного вектора ![]() на k-тую координатную ось
на k-тую координатную ось ![]() . То есть, если
. То есть, если ![]() и
и ![]() - проектор, отображающий
- проектор, отображающий ![]() в
в ![]() , то
, то ![]() является композицией
отображений:
является композицией
отображений:
![]() .
.
Коэффициент линейной
корреляции – мера
статистической силы связи между случайными величинами. Вычисляется по формуле 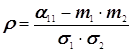 . Применяется в тех
случаях, когда статистическая связь имеет линейный характер.
. Применяется в тех
случаях, когда статистическая связь имеет линейный характер.
Критерий проверки основной гипотезы случайная величина, статистика элементов выборки, закон распределения вероятностей которой зависит от предполагаемой гипотезы.
М
Математическое
ожидание – числовая
характеристика случайной величины, ![]() .
Математическое ожидание есть среднее значение случайной величины
.
Математическое ожидание есть среднее значение случайной величины ![]() . Интерпретируется как
координата центра тяжести единичной массы распределённой на числовой оси.
. Интерпретируется как
координата центра тяжести единичной массы распределённой на числовой оси.
Множество элементарных исходов – множество, элементами, которого является все возможные элементарные исходы. В результате проведения испытания всегда реализуется один, и только один элементарный исход.
Н
Начальный момент k-того порядка – числовая характеристика случайной
величины, являющаяся значением абсолютно сходящегося несобственного интеграла
от функции ![]() по функции распределения
случайной величины, то есть:
по функции распределения
случайной величины, то есть: ![]() .
.
Независимость
случайных величин. Случайные
величины ![]() и
и ![]() называются независимыми,
если закон распределения вероятностей одной из них не зависит от другой
случайной величины.
называются независимыми,
если закон распределения вероятностей одной из них не зависит от другой
случайной величины.
Точнее: пусть случайные
величины ![]() и
и ![]() являются компонентами
двумерной случайной величины
являются компонентами
двумерной случайной величины ![]() ,
принимающей значения в
,
принимающей значения в ![]() . Эти компоненты
называются независимыми, если для любого множества B,
. Эти компоненты
называются независимыми, если для любого множества B,![]() B(
B(![]() 2),
представимого как декартово произведение
2),
представимого как декартово произведение ![]() ,
,
![]() и
и ![]() , будет справедливо:
, будет справедливо:
![]() ,
,
Где ![]() и
и ![]() - частные вероятностные
функции компонент.
- частные вероятностные
функции компонент.
Независимость
случайных величин непрерывного типа – Случайные величины непрерывного типа ![]() и
и ![]() (компоненты двумерного
случайного вектора) будут независимыми тогда, только тогда, когда для любой пары
(компоненты двумерного
случайного вектора) будут независимыми тогда, только тогда, когда для любой пары
![]() выполняется равенство
выполняется равенство ![]() , где
, где ![]() - плотность вероятности
двумерного случайного вектора
- плотность вероятности
двумерного случайного вектора ![]() , а
, а ![]() и
и ![]() - плотности вероятностей
его компонент
- плотности вероятностей
его компонент ![]() и
и ![]() .
.
Независимость
случайных величин дискретного типа – Случайные величины дискретного типа ![]() и
и ![]() (компоненты двумерного
случайного вектора) будут независимыми тогда, только тогда, когда для любой пары
(компоненты двумерного
случайного вектора) будут независимыми тогда, только тогда, когда для любой пары
![]() выполняется равенство
выполняется равенство ![]() , где
, где ![]() , а
, а ![]() и
и ![]() .
.
Независимость
случайных событий. Случайные
события называются независимыми, если условная вероятность наступления любого
из них равна его безусловной вероятности: ![]() или
или
![]() .
.
Непрерывная случайная
величина – случайная
величина, областью возможных значений которой является множество D мощности континуум и положительной меры Лебега. Закон
распределения вероятностей непрерывной случайной величины задаётся путём
определения на этом множестве плотности вероятности ![]() -
кусочно-непрерывной, неотрицательной функции, такой что
-
кусочно-непрерывной, неотрицательной функции, такой что ![]() .
.
Несмещённость точечной
оценки. Точечная
оценка ![]() числовой характеристики
числовой характеристики ![]() называется несмещённой,
если
называется несмещённой,
если ![]() .
.
О
Остаточная дисперсия
мера разброса
значений одной из компонент (например ![]() )
двумерной случайной величины
)
двумерной случайной величины ![]() около е
математического ожидания, вызванного внутренними свойствами этой компоненты.
При линейном виде статистической связи между компонентами величина остаточной
дисперсии компоненты
около е
математического ожидания, вызванного внутренними свойствами этой компоненты.
При линейном виде статистической связи между компонентами величина остаточной
дисперсии компоненты ![]() равна
равна ![]() , где
, где ![]() - коэффициент
линейной корреляции между компонентами
- коэффициент
линейной корреляции между компонентами ![]() и
и
![]() .
.
Ошибка I рода – отклонение верной гипотезы ![]() . Возникает в том случае,
когда при справедливости в реальности гипотезы
. Возникает в том случае,
когда при справедливости в реальности гипотезы ![]() наблюдаемое
значение критерия
наблюдаемое
значение критерия ![]() попадает в
критическую область
попадает в
критическую область ![]() . Вероятность
ошибки I рода равна
. Вероятность
ошибки I рода равна ![]() .
.
Ошибка II рода – принятие неверной гипотезы ![]() . Возникает в том случае,
когда при справедливости в реальности гипотезы
. Возникает в том случае,
когда при справедливости в реальности гипотезы ![]() наблюдаемое
значение критерия
наблюдаемое
значение критерия ![]() попадает в
область допустимых значений
попадает в
область допустимых значений ![]() . Вероятность
ошибки II рода равна
. Вероятность
ошибки II рода равна ![]() .
.
П
Повторные независимые
испытания – серия
одинаковых испытаний, в каждом из которых с постоянными вероятностями p и q может произойти только одно из взаимно
противоположных событий A или
![]() .
.
Плотность вероятности – неотрицательная,
кусочно-непрерывная функция, удовлетворяющая условию: ![]() . Плотность вероятности
описывает распределение вероятностей случайной величины
. Плотность вероятности
описывает распределение вероятностей случайной величины ![]() непрерывного типа.
непрерывного типа.
Р
Распределение ![]() - (распределение Пирсона)
распределение вероятностей случайной величины
- (распределение Пирсона)
распределение вероятностей случайной величины ![]() ,
где все
,
где все ![]() независимые случайные
величины, имеющие нормальное распределение вероятностей N(0;1).
независимые случайные
величины, имеющие нормальное распределение вероятностей N(0;1).
Распределение
Стьюдента – (t-распределение) распределение вероятностей случайной
величины 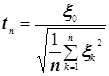 , где все
, где все ![]() независимые случайные
величины, имеющие нормальное распределение вероятностей N(0;1).
независимые случайные
величины, имеющие нормальное распределение вероятностей N(0;1).
Распределение
Фишера-Снедекора – (F-распределение) распределение вероятностей случайной
величины 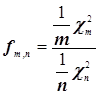 .
.
Ряд распределения – таблица, состоящая из двух строк, с помощью которой задаётся закон распределения дискретной случайной величины:
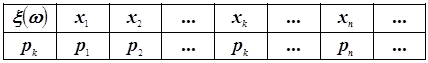 .
.
Где ![]() или
или ![]() ;
; ![]() . Всегда
. Всегда ![]() .
.
С
Свёртка функций
распределения – несобственный
интеграл, определяющий функцию распределения случайной величины, являющейся
суммой независимых случайных величин. Если ![]() ,
то функция распределения
,
то функция распределения ![]() будет
равна:
будет
равна: ![]() , где
, где ![]() и
и ![]() - функции распределения
случайных величин-слагаемых.
- функции распределения
случайных величин-слагаемых.
Состоятельность
точечной оценки. Точечная
оценка ![]() числовой характеристики
числовой характеристики ![]() называется состоятельной,
если она сходится по вероятности к этой точечной оценке, то есть:
называется состоятельной,
если она сходится по вероятности к этой точечной оценке, то есть: ![]() .
.
Статистика – любая функция элементов выборки ![]() :
: ![]() .
.
Сходимость по
вероятности.
Последовательность случайных величин ![]() сходится
по вероятности к случайной величине
сходится
по вероятности к случайной величине ![]() (обозначение:
(обозначение:
![]() ), если выполняется условие
), если выполняется условие
![]() .
.
Сходимость по
распределению.
Последовательность случайных величин ![]() сходится
по распределению к случайной величине
сходится
по распределению к случайной величине ![]() (обозначение:
(обозначение:
![]() ), если соответствующая
последовательность функций распределения
), если соответствующая
последовательность функций распределения ![]() слабо
сходится к функции распределения
слабо
сходится к функции распределения ![]() случайной
величины
случайной
величины ![]() (
(![]() ).
).
У
Условная вероятность ![]() - вероятность наступления случайного
события A, вычисленная при предположении, что
случайное событие B
произошло. Определяется по формуле:
- вероятность наступления случайного
события A, вычисленная при предположении, что
случайное событие B
произошло. Определяется по формуле: 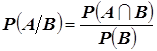 .
.
Условная плотность
вероятности ![]() - плотность вероятности условной
случайной величины
- плотность вероятности условной
случайной величины ![]() , является
законом распределения вероятностей второй компоненты при любом фиксированном
значении первой компоненты. Определяется по формуле:
, является
законом распределения вероятностей второй компоненты при любом фиксированном
значении первой компоненты. Определяется по формуле: 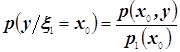 , где
, где ![]() - плотность вероятности
двумерной случайной величины
- плотность вероятности
двумерной случайной величины ![]() ,
, ![]() - частная плотность
вероятности первой компоненты
- частная плотность
вероятности первой компоненты ![]() .
.
Ф
Функция распределения
функция ![]() , описывающая изменение
вероятности случайного события
, описывающая изменение
вероятности случайного события ![]() при
изменении x, то есть
при
изменении x, то есть ![]() .
Определяя функцию распределения
.
Определяя функцию распределения ![]() , мы
задаём закон распределения вероятностей случайной величины
, мы
задаём закон распределения вероятностей случайной величины ![]() .
.
Функция распределения
вектора - функция ![]() , описывающая изменение вероятности
случайного события
, описывающая изменение вероятности
случайного события ![]() , где
, где ![]() , при изменении
, при изменении ![]() , то есть
, то есть ![]() .
Определяя функцию распределения
.
Определяя функцию распределения ![]() , мы
задаём закон распределения вероятностей случайного вектора
, мы
задаём закон распределения вероятностей случайного вектора ![]() .
.
Функция регрессии – функция, описывающая зависимость
значений условных математических ожиданий одной из компонент двумерной случайной
величины от другой компоненты. Функция![]() -
функция регрессии компоненты
-
функция регрессии компоненты ![]() на
изменение компоненты
на
изменение компоненты ![]() . Функция
. Функция![]() - функция регрессии
компоненты
- функция регрессии
компоненты ![]() на изменение компоненты
на изменение компоненты ![]() .
.
Х
Характеристическая
функция – комплексно-значная
функция действительного аргумента, являющаяся математическим ожиданием функции ![]() случайной величины
случайной величины ![]() , где
, где ![]() , то есть:
, то есть: ![]() .
.
Ч
Частная функция
распределения – функция
распределения любой k-той
компоненты ![]() вектора
вектора ![]() . Определение частной
функции распределения основано на свойстве согласованности функции распределения
многомерной случайной величины, например, если n=2, то
. Определение частной
функции распределения основано на свойстве согласованности функции распределения
многомерной случайной величины, например, если n=2, то ![]() и
и ![]() .
.
Частные распределения
компонент случайного вектора - распределения вероятностей компонент вектора, являющихся
скалярными случайными величинами. Частное распределение каждой компоненты
получается как проекция вероятностной функции вектора на соответствующую
координатную ось. Если ![]() и P вероятностная функция вектора, то
частное распределение
и P вероятностная функция вектора, то
частное распределение ![]() компоненты
компоненты ![]() определяется равенством:
определяется равенством: ![]() , где
, где ![]() B(
B(![]() ). Аналогично, частное
распределение
). Аналогично, частное
распределение ![]() компоненты
компоненты ![]() определяется равенством:
определяется равенством: ![]() , где
, где ![]() B(
B(![]() ).
).
Ц
Центральная предельная
теорема (ЦПТ) – совокупность
теорем, в которых на последовательность случайных величин ![]() , налагаются условия, при
которых их центрированная и нормированная сумма
, налагаются условия, при
которых их центрированная и нормированная сумма 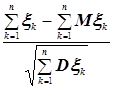 сходится по распределению
к нормальному закону N(0;1).
сходится по распределению
к нормальному закону N(0;1).
Э
Эффективная оценка – точечная оценка числовой характеристики, имеющая наименьшую дисперсию.
VIII. Вопросы для тестирования по курсу
«Теория вероятностей и математическая статистика»
1. Противоположным событием случайному
событию ![]() будет событие: а) событие
будет событие: а) событие ![]() ; б) событие
; б) событие ![]() ; в) событие
; в) событие ![]() .
.
2.Вероятности наступления
случайных событий ![]() и
и ![]() равны
равны ![]() и
и ![]() . Эти случайные события: а)
совместные; б) несовместные; в) взаимно противоположные.
. Эти случайные события: а)
совместные; б) несовместные; в) взаимно противоположные.
3.Гипотезы, формулируемые при применении формулы полной вероятности, должны быть: а) попарно независимыми; б) попарно несовместными; в) взаимно противоположными.
4.Аддитивная функция
множеств ![]() и
и ![]() удовлетворяет условию: а)
всегда
удовлетворяет условию: а)
всегда ![]() , если
, если ![]() ;
;
б) всегда ![]() , если
, если ![]() ;
;
в) всегда ![]() , если
, если ![]() .
.
5. Требование счётной аддитивности числовой функции множеств это: а) аксиоматическое требование, объявляемое при определении вероятностной функции;
б) необходимое требование, объявляемое при определении независимости случайных величин;
в) достаточное требование, выполнение которого проверяется при определении алгебры борелевских множеств.
6. Случайная величина это: а) случайный результат любого опыта;
б) измеримое отображение множества элементарных исходов во множество чисел;
в) вероятность наступления случайного события при однократном проведении опыта.
7. Плотность вероятности ![]() это:
это:
а) функция, для которой
при любых неотрицательных a
и b интеграл 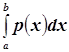 принимает
конечные значения;
принимает
конечные значения;
б) любая функция, для
которой справедливо 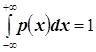 ;
;
в) любая функция, которая
удовлетворяет двум условиям: ![]() для
любого x,
для
любого x, ![]() ,
и
,
и 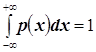 .
.
8. Математическое ожидание случайной величины это:
а) наиболее вероятное значение случайной величины;
б) среднее значение случайной величины;
в) ожидаемое значение случайной величины.
9. Дисперсия случайной величины это:
а) разброс возможных значений случайной величины около её математического ожидания;
б) мера разброса возможных значений случайной величины около её математического ожидания;
в) мера связи возможных значений случайной величины и её математического ожидания.
10. Дисперсия разности
случайных величин ![]() и
и ![]() равна:
равна:
а) ![]() , если случайные величины
независимые;
, если случайные величины
независимые;
б) ![]() , если случайные величины
несовместные;
, если случайные величины
несовместные;
в)![]() , если случайные величины
произвольные;
, если случайные величины
произвольные;
11. Независимость случайных величин определяется исходя из:
а) невозможности определения закона совместного распределения компонент случайного вектора;
б) равенства закона распределения случайного вектора произведению законов распределения его компонент;
в) невыполнения всех условий теоремы Чебышева.
12. Функция Лапласа используется при:
а) определении величины разброса значений случайной величины при проведении большого числа наблюдений;
б) определении вероятностей событий, которые могут наступить при проведении больших серий повторных независимых испытаний;
в) при вычислении значений статистических оценок коэффициентов функции регрессии.
13. Функция Лапласа применяется при:
а) определении математического ожидания нормально распределённой случайной величины;
б) проверке статистической гипотезы о виде закона распределения случайной величины;
в) вычислении вероятностей наступления случайных событий, определяемых нормально распределённой случайной величиной.
14. Коэффициент линейной корреляции используется для определения:
а) величины разброса значений одной из случайных величин около математического ожидания другой случайной величины;
б) силы статистической связи между значениями случайных величин;
в) меры зависимости условного распределения одной из компонент случайного вектора от частного распределения другой компоненты.
15. Функция регрессии это:
а) функция, описывающая изменение значений одной из случайных величин в зависимости от изменения закона распределения вероятностей другой;
б) функция, описывающая изменение значений условного математического ожидания одной из случайных величин в зависимости от изменения значений другой случайной величины;
в) функция, описывающая зависимость условных математических ожиданий компонент двумерной случайной величины.
16. Закон больших чисел это:
а) совокупность теорем, в которых на последовательность случайных величин накладываются условия, при которых их центрированная и нормированная сумма с вероятностью близкой к единице принимает значения, мало отличающиеся от нуля;
б) закон, определяющий распределение вероятностей больших отклонений от нуля;
в) закон, оценивающий большие отклонения значений случайных величин от их математического ожидания.
17. Остаточная дисперсия:
а) оценивает разброс значений одной из компонент двумерной случайной величины около е математического ожидания, вызванный её внутренними свойствами;
б) оценивает разброс значений одной из компонент двумерной случайной величины около математического ожидания другой компоненты;
в) оценивает разброс значений центрированной компоненты двумерной случайной величины около условного математического ожидания другой компоненты.
18. Для определения точечных оценок числовых характеристик случайной величины необходимо:
а) иметь выборку из генеральной совокупности;
б) построить гистограмму распределения относительных частот;
в) применить метод наименьших квадратов.
19. «Рассматривается последовательность независимых, как угодно распределённых случайных величин, дисперсии которых ограничены одной общей константой,…». Эти требования к случайным величинам формулируются:
а) в теореме Леви;
б) в теореме Ляпунова;
в) в теореме Чебышева.
20. «Состоятельность» это:
а) одно из требований, предъявляемое к точечным оценкам числовых характеристик случайных величин;
б) требование к статистикам, необходимым при определении границ доверительного интервала;
в) требование, выполнение которого позволяет минимизировать вероятность ошибки первого рода при статистической проверке гипотез.
21. Статической оценкой математического ожидания случайной величины является:
а) нормированная сумма наблюдаемых значений случайной величины;
б) среднее арифметическое элементов выборки наблюдаемых значений случайной величины;
в) среднее арифметическое максимального и минимального значений элементов выборки.
22. Доверительный интервал это:
а) интервал наиболее вероятных значений случайной величины;
б) интервал значений вероятностей практически достоверных событий;
в) интервал, в котором с доверительной вероятностью находится числовая характеристика случайной величины.
23. Центральная предельная теорема это:
а) терема о предельном распределении последовательности центрированных случайных величин;
б) совокупность теорем, в которых на последовательность случайных величин накладываются условия, при которых их центрированная и нормированная сумма подчиняются распределению мало отличающемуся от нормального.
в) общая теорема о существовании центрированного распределения вероятностей для предельных значений случайных величин.
24. Критерий статистической проверки гипотез является:
а) случайной величиной, значения которой зависят от элементов генеральной совокупности, попавших в выборку;
б) числовой характеристикой эмпирической случайной величины;
в) областью возможных значений проверяемой гипотезы.
25. Критерий статистической проверки гипотез это:
а) случайная величина, значения которой позволяют подтвердить или опровергнуть основную гипотезу;
б) случайная величина, распределение которой зависит от формулировки проверяемых гипотез;
в) случайная величина, по распределению вероятностей которой проверяется гипотеза о независимости основной и альтернативной гипотез.
26. Теорема Чебышёва является предельной теоремой:
а) для последовательности дискретных случайных величин;
б) для последовательности непрерывных случайных величин;
в) для последовательности случайных величин, независимо от типа законов распределения их вероятностей.
27. По результатам
проверки по элементам одной и той же выборки значений ![]() двух гипотез
двух гипотез
![]() ,
,
![]() ,
,
где ![]() и
и ![]() - разные функции
распределения, приято решение о том, что нет оснований отклонять и первую, и
вторую гипотезу.
- разные функции
распределения, приято решение о том, что нет оснований отклонять и первую, и
вторую гипотезу.
а) При применении критерия Пирсона такого решения не может быть.
б) При применении критерия Пирсона такое решение может быть.
в) Такое решение может
быть только в том случае, если случайная величина ![]() принимает
только положительные значения.
принимает
только положительные значения.
ОТВЕТЫ К ТЕСТАМ