
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Дипломная работа: Систематичний відбір
Дипломная работа: Систематичний відбір
Міністерство освіти і науки України
Дніпропетровський національний університет ім. О. Гончара
Дипломна бакалаврська робота
Систематичний відбір
Виконавець:
студентка групи
МС-06-1 Бабічева Д.С.
Дніпропетровськ 2010
РЕФЕРАТ
Випускна бакалаврська робота: 67 сторінок, 5 джерел, 9 таблиць, 15 рисунків.
Перелік ключових слів: популяція, вибірка, відбір, дисперсія, середнє, точність, тренд, одиниці, оцінка.
Обє’кт дослідження: систематичні вибірки
Мета роботи: в роботі ставиться задача порівняння точності систематичного відбору, простого випадкового відбору та стратифікованого відбору на прикладі вибіркового обстеження домогосподарств гіпотетичного міста StatVillage.
ЗМІСТ
ВСТУП
РОЗДІЛ І. СИСТЕМАТИЧНИЙ ВІДБІР
1.1 Оцінювання середнього та сумарного значення популяції
1.2 Порівняння систематичного відбору зі стратифікованим випадковим відбором
1.3 Популяції з «випадковим» порядком розміщення одиниць
1.4 Популяції з лінійним трендом
1.5 Популяції з періодичною варіацією
1.6 Автокорельовані популяції
1.7 Реальні популяції
1.8 Оцінювання дисперсії за окремою вибіркою
1.9 Стратифікований систематичний відбір
1.10 Двовимірний систематичний відбір
1.11 Приклади розв’язування задач
РОЗДІЛ ІІ. ПОРІВНЯННЯ СИСТЕМАТИЧНОГО ВІДБОРУ, ПРОСТОГО ВИПАДКОВОГО ВІДБОРУ ТА СТРАТИФІКРВАНОГО ВІДБОРІВ
2.1 Місто StatVillage
2.2 Порівняння відборів
ВИСНОВКИ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
ВСТУП
Вибіркове обстеження з
систематичним відбором являє собою комплекс процедур, які мають деякі практичн
переваги за інших методів, зокрема у відносній простоті застосування. Інод
систематичний відбір розглядають як деяке наближення простого випадкового
відбору, коли не існує повного переліку або списку всієї популяції, або коли
цей список не є впорядкованим за якоюсь ознакою, тобто коли елементи записано в
довільному випадковому порядку. Розглянемо загальну процедуру побудови
систематичної вибірки при проведенні випадкового обстеження. Нехай маємо
скінчену популяцію, одиниці якої перенумеровані від 1 до ![]() . Для отримання вибірки
обсягу
. Для отримання вибірки
обсягу ![]() спочатку навмання
вибираємо будь-яку одиницю з перших
спочатку навмання
вибираємо будь-яку одиницю з перших ![]() одиниць
популяції (це можна зробити, використовуючи датчик випадкових чисел або таблицю
випадкових чисел). Після вибору першої одиниці вибираємо кожну
одиниць
популяції (це можна зробити, використовуючи датчик випадкових чисел або таблицю
випадкових чисел). Після вибору першої одиниці вибираємо кожну ![]() -ту одиницю популяції. Таку
вибірку будемо називати систематичною вибіркою кожної
-ту одиницю популяції. Таку
вибірку будемо називати систематичною вибіркою кожної ![]() -ї одиниці. Наприклад,
якщо
-ї одиниці. Наприклад,
якщо ![]() =15 і першу одиницю
виберемо 13, тоді наступні одиниці будуть мати номери 28, 43, 58, 73... Отже,
перша вибрана одиниця повністю визначає вибірку. У систематичного відбору
деякі очевидні переваги в порівнянні з простим випадковим відбором.
=15 і першу одиницю
виберемо 13, тоді наступні одиниці будуть мати номери 28, 43, 58, 73... Отже,
перша вибрана одиниця повністю визначає вибірку. У систематичного відбору
деякі очевидні переваги в порівнянні з простим випадковим відбором.
1.
Вибірку
легше добувати і частіше легше дотримуватись правил відбору. Це особливо важливо,
коли відбір відбувається безпосередньо протягом обстеження. Іноді можна значно
зекономити час, навіть коли вибірка добувається до початку обстеження.
Наприклад, коли данні про всі одиниці занесені на картки однакового розміру, що
знаходяться у ящиках стандартної картотеки. Тоді можна добувати картки з ящика
через кожний сантиметр, відміряючи відстань лінійкою. Цю операцію, на відміну
від простого випадкового відбору, можна виконати дуже швидко. Звичайно, такий
метод трохи відрізняється від відбору строго кожної ![]() -то
картки.
-то
картки.
2.
Інтуїтивно
систематичний відбір здається більш точним, ніж простий випадковий відбір. По
суті, при відборі відбувається стратифікування популяції на n страт, що
складаються з перших ![]() одиниць, з
других
одиниць, з
других ![]() одиниць і т.д. Отже, ми
могли б очікувати, що систематична вибірка має приблизну ту саму точність, що
відповідна стратифікована вибірка з однією одиницею в кожній страті.
Відмінність між ними полягає в тому, що при систематичному відборі одиниця в
кожній страті стоїть на одному і тому самому місці відносно інших одиниць, у
той час як, при стратифікованому випадковому відборі її місце в страт
визначається навмання окремо для кожної страти (див. рис.1). Систематична
вибірка розподілена в популяції більш рівномірно і саме це робить інод
систематичний відбір більш точним, ніж стратифікований випадковий відбір.
одиниць і т.д. Отже, ми
могли б очікувати, що систематична вибірка має приблизну ту саму точність, що
відповідна стратифікована вибірка з однією одиницею в кожній страті.
Відмінність між ними полягає в тому, що при систематичному відборі одиниця в
кожній страті стоїть на одному і тому самому місці відносно інших одиниць, у
той час як, при стратифікованому випадковому відборі її місце в страт
визначається навмання окремо для кожної страти (див. рис.1). Систематична
вибірка розподілена в популяції більш рівномірно і саме це робить інод
систематичний відбір більш точним, ніж стратифікований випадковий відбір.

Рис.1. Систематичний відбір
та стратифіксований випадковий відбір: ![]() -
систематична вибірка,
-
систематична вибірка, ![]() -
стратифікована вибірка
-
стратифікована вибірка
В одному з варіантів
систематичного відбору кожна одиниця відбирається в центрі страти або біля
нього, тобто замість того, щоб починати послідовність номерів деяким випадковим
чином від 1 до ![]() , ми приймаємо
номер першої одиниці рівним
, ми приймаємо
номер першої одиниці рівним ![]() , якщо
, якщо ![]() – непарне, та
– непарне, та ![]() або
або ![]() , якщо
, якщо ![]() – парне число. Такий
прийом доводить ідею систематичного відбору до її логічного завершення. У тому
випадку, коли
– парне число. Такий
прийом доводить ідею систематичного відбору до її логічного завершення. У тому
випадку, коли ![]() можна розглядати
як значення неперервної функції від неперервного аргумента
можна розглядати
як значення неперервної функції від неперервного аргумента ![]() , є підстави очікувати, що
вибірка, яка розташована центрально, буде більш точною, ніж випадково
розташована. Проте ефективність центрально розташованих вибірок для типів популяцій,
що зазвичай зустрічаються при вибіркових обстеженнях, вивчена недостатньо, тому
обмежимося випадково розташованими вибірками.
, є підстави очікувати, що
вибірка, яка розташована центрально, буде більш точною, ніж випадково
розташована. Проте ефективність центрально розташованих вибірок для типів популяцій,
що зазвичай зустрічаються при вибіркових обстеженнях, вивчена недостатньо, тому
обмежимося випадково розташованими вибірками.
Оскільки, взагалі кажучи, ![]() не є цілим кратним числа
не є цілим кратним числа ![]() , обсяги різних
систематичних вибірок з однієї і тієї ж популяції можуть на одиницю
відрізнятись один від одного. Так, наприклад, для
, обсяги різних
систематичних вибірок з однієї і тієї ж популяції можуть на одиницю
відрізнятись один від одного. Так, наприклад, для ![]() =
23,
=
23, ![]() = 5 в таблиці 1 вказан
номери одиниць для п’яти систематичних вибірок. Перші три вибірки мають обсяг
= 5 в таблиці 1 вказан
номери одиниць для п’яти систематичних вибірок. Перші три вибірки мають обсяг ![]() = 5, а дві останні – обсяг
= 5, а дві останні – обсяг
![]() = 4. Ці обставини вносять
деякі ускладнення в теорію систематичного відбору. Якщо обсяг
= 4. Ці обставини вносять
деякі ускладнення в теорію систематичного відбору. Якщо обсяг ![]() перевищує 50, то цим
ускладненням можна знехтувати. Навіть при малих обсягах
перевищує 50, то цим
ускладненням можна знехтувати. Навіть при малих обсягах ![]() зміни будуть незначні. Але
якщо за оцінку середнього значення популяції вибрати середнє арифметичне тако
систематичної вибірки, то ця оцінка буде зміщеною.
зміни будуть незначні. Але
якщо за оцінку середнього значення популяції вибрати середнє арифметичне тако
систематичної вибірки, то ця оцінка буде зміщеною.
Таблиця 1 Можлив
систематичні вибірки при ![]() = 23,
= 23, ![]() = 5
= 5
| Номер систематичної вибірки | ||||
| перша | друга | третя | четверта | п’ята |
|
1 6 11 16 21 |
2 7 12 17 22 |
3 8 13 18 23 |
4 9 14 19 |
5 10 15 20 |
Для того, щоб уникнути цього,
можна скористатися таким методом. Вибираємо ![]() як
найбільше ціле, що лежить поряд
як
найбільше ціле, що лежить поряд ![]() . Далі навмання
вибираємо будь-яку одиницю від 1 до
. Далі навмання
вибираємо будь-яку одиницю від 1 до ![]() , потім
беремо кожну
, потім
беремо кожну ![]() -у одиницю, рухаючись по
колу, поки не виберемо
-у одиницю, рухаючись по
колу, поки не виберемо ![]() одиниць. Наприклад,
одиниць. Наприклад,
![]() = 21,
= 21, ![]() = 5, тоді
= 5, тоді ![]() = 4. Нехай вибрано одиницю
з номером 13. Тоді систематична вибірка 4-го порядку буде містити одиниці з
номерами: 13, 17, 21, 4, 8. Якщо першу одиницю вибрано з номером 19, то вибірка
містить одиниці з номерами: 19, 2, 6, 10, 14.
= 4. Нехай вибрано одиницю
з номером 13. Тоді систематична вибірка 4-го порядку буде містити одиниці з
номерами: 13, 17, 21, 4, 8. Якщо першу одиницю вибрано з номером 19, то вибірка
містить одиниці з номерами: 19, 2, 6, 10, 14.
В роботі ставиться задача порівняння точності систематичного відбору, простого випадкового відбору та стратифікованого відбору на прикладі вибіркового обстеження домогосподарств гіпотетичного міста StatVillage.
РОЗДІЛ І. СИСТЕМАТИЧНИЙ ВІДБІР
1.1 Оцінювання середнього та сумарного значення популяції
Введемо поняття кластеру.
Кластер – це група одиниць популяції, яка розглядається як вихідна одиниця
вибірки. Нехай ![]() . Популяцію можна
розбити на
. Популяцію можна
розбити на ![]() кластерів, у кожному з
яких знаходиться n одиниць. Тоді процедура випадкового відбору систематично
вибірки
кластерів, у кожному з
яких знаходиться n одиниць. Тоді процедура випадкового відбору систематично
вибірки ![]() го порядку така ж сама, як
процедура вибору одного із
го порядку така ж сама, як
процедура вибору одного із ![]() кластерів
(див. табл. 1.1.1).
кластерів
(див. табл. 1.1.1).
Таблиця 1.1.1 Можлив
систематичні вибірки ![]() го порядку
го порядку
| Страти | Кластер | Середн страти | |||||
| 1 | 2 | … | i | … | k | ||
| 1 |
|
|
… |
|
… |
|
|
| 2 |
|
|
… |
|
… |
|
|
| … | … | … | … | … | … | … | … |
|
|
|
|
… |
|
… |
|
|
| Середнє систематично вибірки |
|
|
… |
|
… |
|
|
Нехай випадкова величина ![]() – середнє значення систематично
вибірки, тобто
– середнє значення систематично
вибірки, тобто ![]() з імовірністю
з імовірністю ![]() дорівнює значенню
дорівнює значенню ![]() ,
, ![]() .
.
Розподіл ![]() має вигляд
має вигляд
![]() ~
~![]() .
.
Теорема 1.1.1. Середнє значення ![]() систематичної вибірки
незміщеною оцінкою для середнього значення популяції
систематичної вибірки
незміщеною оцінкою для середнього значення популяції ![]() .
.
Доведення.
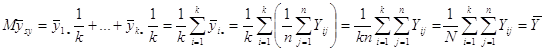 ,
,
де ![]() -ий член
-ий член ![]() -тої систематичної вибірки,
-тої систематичної вибірки,
![]() ,
, ![]() ,
,
зокрема, дисперсія ![]() дорівнює
дорівнює
![]() .
.
Теорема доведена.
Теорема 1.1.2. Дисперсія середнього значення систематичної вибірки визначається формулою
![]() (1.1.1)
(1.1.1)
Де
![]()
є дисперсією одиниць, як належать одній систематичній вибірці (wsy − від англ. within − всередині та systematic − систематичний).
Доведення.
Дисперсія популяції з ![]() одиниць визначається
формулою
одиниць визначається
формулою
![]() .
.
Розглянемо тотожність
![]() .
.
Піднесемо обидві частини рівності до квадрату
![]() .
.
Підсумуємо праву та ліву
частини рівності за ![]() та
та ![]() :
:
![]()
![]()
Покажемо, що ![]() :
:
![]()
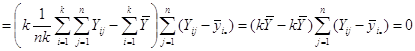
Отже, маємо
![]() ,
,
![]() .
.
Дисперсія ![]() дорівнює
дорівнює
![]()
(обчислена за таблицею
розподілу ![]() ). Тоді
). Тоді
![]() .
.
Звідси
![]() ,
,
або, що теж саме,
![]() .
.
Теорема доведена.
Наслідок. Середнє значення для систематичної вибірки більш точне, ніж середнє для простої випадкової вибірки, тобто
![]()
тоді і тільки тоді, коли
![]() . (1.1.2)
. (1.1.2)
Доведення.
Дисперсія середнього значення простої випадкової вибірки дорівнює
![]() .
.
Тоді з (1.1.1) випливає, що ![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]() .
.
Звідси маємо
![]() .
.
Домножимо обидві частини
нерівності на ![]() та праворуч
винесемо
та праворуч
винесемо ![]() :
:
![]() .
.
Враховуючи, що ![]() маємо
маємо
![]() ,
,
або,
![]() .
.
Отже , ![]() .
.
Наслідок доведено.
Таким чином, систематичний відбір
точніший, ніж простий випадковий відбір, якщо дисперсія ![]() одиниць систематичних
вибірок більша дисперсії
одиниць систематичних
вибірок більша дисперсії ![]() вс
популяції. Систематичний відбір точний, коли одиниці всередині однієї й тієї ж
вибірки неоднорідні, та неточний, коли вони однорідні. До цього можна прийти
нтуїтивно. Якщо всередині систематичної вибірки варіація у порівнянні з
варіацією популяції невелика, то послідовно вибрані одиниці вибірки несуть
більш або менш однакову інформацію. Інший вираз для дисперсії наведемо у
теоремі 1.1.3.
вс
популяції. Систематичний відбір точний, коли одиниці всередині однієї й тієї ж
вибірки неоднорідні, та неточний, коли вони однорідні. До цього можна прийти
нтуїтивно. Якщо всередині систематичної вибірки варіація у порівнянні з
варіацією популяції невелика, то послідовно вибрані одиниці вибірки несуть
більш або менш однакову інформацію. Інший вираз для дисперсії наведемо у
теоремі 1.1.3.
Теорема 1.1.3.
![]() , (1.1.3)
, (1.1.3)
де ![]() - коефіцієнт кореляц
між парами одиниць, що належать до однієї й тієї самої систематичної вибірки.
Цей коефіцієнт визначається за формулою
- коефіцієнт кореляц
між парами одиниць, що належать до однієї й тієї самої систематичної вибірки.
Цей коефіцієнт визначається за формулою
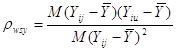 ,
,
де чисельник є середнім по
всім ![]() різним парам, а знаменник
середнє по всім
різним парам, а знаменник
середнє по всім ![]() значенням
значенням ![]() . Розпишемо чисельник
знаменник:
. Розпишемо чисельник
знаменник:
![]()
![]()
Підставивши отримані вирази у
![]() отримаємо:
отримаємо:
![]() .
.
Доведення.
Дисперсія середнього значення
![]() систематичної вибірки
дорівнює
систематичної вибірки
дорівнює
![]() .
.
Звідси маємо
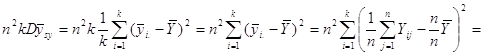
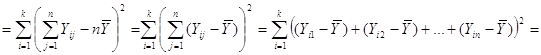
![]()
![]() .
.
Отже,
![]()
![]() .
.
Ділимо обидві частини на ![]() і отримуємо вираз для
і отримуємо вираз для ![]()
![]()
![]() .
.
Останній результат показує,
що додатна кореляція між одиницями в одній і тій самій вибірці збільшує дисперсію
вибіркового середнього. Навіть мала додатна кореляція може мати великий ефект
за рахунок множника ![]() .
.
Теорема доведена.
Дві попередні теореми
виражали ![]() через дисперсію популяції
через дисперсію популяції ![]() , тобто співвідносили
дисперсію
, тобто співвідносили
дисперсію ![]() з дисперсією для просто
випадкової вибірки
з дисперсією для просто
випадкової вибірки
![]() .
.
Існує аналог теореми 1.1.3, в
якому ![]() виражена через дисперсію стратифіковано
випадкової вибірки, де страти складалися з перших
виражена через дисперсію стратифіковано
випадкової вибірки, де страти складалися з перших ![]() одиниць,
других
одиниць,
других ![]() одиниць і т.п. При
позначеннях індекс
одиниць і т.п. При
позначеннях індекс ![]() при
при ![]() відповідає номеру страти.
Середнє для страти будемо записувати так
відповідає номеру страти.
Середнє для страти будемо записувати так ![]() .
.
Теорема 1.1.4.
![]() , (1.1.4)
, (1.1.4)
![]()
![]() – дисперсія одиниць, що
належать до однієї й тієї самої страти. В знаменнику стоїть
– дисперсія одиниць, що
належать до однієї й тієї самої страти. В знаменнику стоїть ![]() , тому що кожна з
, тому що кожна з ![]() страт вносить
страт вносить ![]() ступінь вільності. Величина
ступінь вільності. Величина
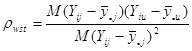 .
.
є коефіцієнтом кореляції між відхиленнями від середнього значення для страти по всім парам одиниць, що належать до однієї й тієї ж систематичної вибірки.
![]() . (1.1.5)
. (1.1.5)
Доведення.
Доведення цієї теореми аналогічно доведенню теореми 1.1.3.
Дисперсія середнього значення
![]() систематичної вибірки
дорівнює
систематичної вибірки
дорівнює
![]()
Розпишемо середнє значення
популяції ![]() через середн
стратифікованої вибірки
через середн
стратифікованої вибірки ![]() :
:
![]() {
{![]() -
це
-
це ![]() -та одиниця
-та одиниця ![]() -ї страти}
-ї страти}![]()
![]() .
.
Отже маємо
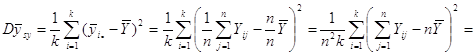
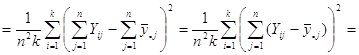
![]()
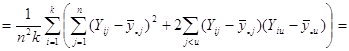
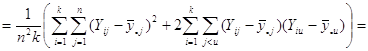
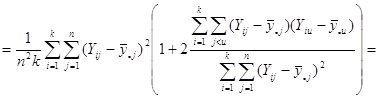
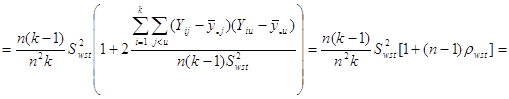
![]() .
.
Отже,
![]() .
.
Теорема доведена.
Наслідок. Якщо ![]() , то систематична вибірка
має ту саму точність, що й відповідна стратифікована випадкова вибірка з однією
одиницею у кожній страті.
, то систематична вибірка
має ту саму точність, що й відповідна стратифікована випадкова вибірка з однією
одиницею у кожній страті.
Це твердження випливає з
того, що для такої стратифікованої випадкової вибірки ![]() дорівнює:
дорівнює:
![]() .
.
Теорема 1.1.5. Дисперсія величини ![]() , яка використовується для
оцінювання сумарного значення популяції
, яка використовується для
оцінювання сумарного значення популяції ![]() ,
дорівнює
,
дорівнює
![]() .
.
Приклад. У таблиці 1.1.2 наведен
данні для невеликої штучної популяції, яка показує тенденцію до досить стійкого
зростання значень ознаки у послідовності одиниць. Маємо ![]() ,
, ![]() ,
, ![]() . Кожний стовпчик
відповідає деякій систематичній вибірці, а рядки є стратами. Приклад ілюстру
ситуацію, коли кореляція «всередині страт» додатна. Наприклад, у першій вибірц
кожне з чотирьох чисел (0, 6, 18, 26) менше середнього значення у страті, до
якого воно належить. Це справедливо, з невеликим винятком, для перших п’яти
систематичних вибірок. В останніх п’яти вибірках відхилення від середніх
значень для страт в основному додатне. Таким чином, члени суми у виразі для
. Кожний стовпчик
відповідає деякій систематичній вибірці, а рядки є стратами. Приклад ілюстру
ситуацію, коли кореляція «всередині страт» додатна. Наприклад, у першій вибірц
кожне з чотирьох чисел (0, 6, 18, 26) менше середнього значення у страті, до
якого воно належить. Це справедливо, з невеликим винятком, для перших п’яти
систематичних вибірок. В останніх п’яти вибірках відхилення від середніх
значень для страт в основному додатне. Таким чином, члени суми у виразі для ![]() переважно додатні.
Відповідно до теореми 1.1.4 можна очікувати, що систематичний відбір буде менш
точним, ніж стратифікований випадковий відбір з однією одиницею у кожній
страті.
переважно додатні.
Відповідно до теореми 1.1.4 можна очікувати, що систематичний відбір буде менш
точним, ніж стратифікований випадковий відбір з однією одиницею у кожній
страті.
Таблиця 1.1.2 Данні по 10
систематичним вибіркам при обсязі вибірок ![]() та
обсязі популяції
та
обсязі популяції![]()
| Страта |
Номер
систематичної вибірки ( |
|
|||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|
I II III IV |
0 6 18 26 |
1 8 19 30 |
1 9 20 31 |
2 10 20 31 |
5 13 24 33 |
4 12 23 32 |
7 15 25 35 |
7 16 28 37 |
8 16 29 38 |
6 17 27 38 |
4,1 12,2 23,3 33,1 |
|
|
12, 5 | 14, 75 | 15, 25 | 15, 75 | 18, 75 | 17, 75 | 20, 5 | 22 | 22, 75 | 22 | 72,7 |
|
|
50 | 58 | 61 | 63 | 75 | 71 | 82 | 88 | 91 | 88 | |
Середнє значення систематичної вибірки має розподіл
![]() ~
~ 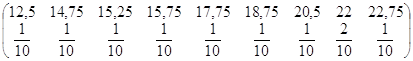
![]()
![]()
Дисперсія систематично вибірки дорівнює
![]()
Знайдемо середнє та дисперсію для всієї популяції:
![]()
![]()
Тепер знайдемо дисперсію одиниць, що належать до однієї й тієї самої страти:
![]() ,
,
де ![]() - число страт,
- число страт, ![]() - обсяг стратифіковано
вибірки.
- обсяг стратифіковано
вибірки.
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
![]() ,
,
де ![]() - обсяг простої випадково
вибірки.
- обсяг простої випадково
вибірки.
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
![]() ,
,
де ![]() - число страт.
- число страт.
Стратифікований випадковий відбір та систематичний відбір виявились набагато ефективнішими, ніж простий випадковий відбір, причому, як і очікувалось, систематичний відбір менш точний, ніж стратифікований випадковий відбір.
1.2 Порівняння систематичного відбору зі стратифікованим випадковим відбором
Ефективність систематичного
відбору в порівнянні зі стратифікованим або простим випадковим відбором суттєво
залежить від особливостей популяції. Існують такі популяції, в яких систематичний
відбір дає високу точність, але є й такі, для яких простий випадковий відбір
більш точним ніж систематичний. Для деяких популяцій та деяких значень ![]() дисперсія
дисперсія ![]() середнього систематично
вибірки, веде себе досить погано − вона може навіть зростати при
збільшені обсягу вибірки
середнього систематично
вибірки, веде себе досить погано − вона може навіть зростати при
збільшені обсягу вибірки ![]() . Тому
важко вказати загальні умови, за яких рекомендовано застосовувати систематичний
відбір. В будь-якому випадку для того, щоб його застосування було ефективним,
необхідно знати будову популяції, з якої проводиться відбір.
. Тому
важко вказати загальні умови, за яких рекомендовано застосовувати систематичний
відбір. В будь-якому випадку для того, щоб його застосування було ефективним,
необхідно знати будову популяції, з якої проводиться відбір.
При дослідженні цієї проблеми
снує два напрямки. При одному з них порівнюються різні типи відбору зі штучних
сукупностей, для яких ![]() є деякою простою
функцією
є деякою простою
функцією ![]() . При іншому − проводиться
аналогічне порівняння для реальних популяцій.
. При іншому − проводиться
аналогічне порівняння для реальних популяцій.
1.3 Популяції з «випадковим» порядком розміщення одиниць
Систематичний відбір,
оскільки він зручний, застосовується іноді до популяцій, в яких одиниці дійсно
розташовані навмання. Наприклад, так буває при відборі з картотеки, що складена
в алфавітному порядку за прізвищами, якщо змінюється ознака, яка ніяк не
пов’язана з прізвищем того, кого обстежують. В цьому випадку не буде ніяко
тенденції чи стратифікування по ![]() в
розташуванні карток, ні кореляції між сусідніми одиницями.
в
розташуванні карток, ні кореляції між сусідніми одиницями.
У такій ситуації ми могли б очікувати,
що систематичний відбір буде, по суті, рівносильний простому випадковому
відбору та буде мати ту саму дисперсію. Для конкретної скінченої популяції при
заданих значеннях ![]() і
і ![]() це не завжди вірно, тому
що
це не завжди вірно, тому
що ![]() , яка має
, яка має ![]() ступенів вільності, при
малих
ступенів вільності, при
малих ![]() досить нестійка і може
виявитись як більше так і менше, ніж
досить нестійка і може
виявитись як більше так і менше, ніж ![]() . Але
снують дві теореми, які показують, що в середньому ці дисперсії рівні.
. Але
снують дві теореми, які показують, що в середньому ці дисперсії рівні.
Теорема 1.3.1. Розглянемо всі ![]() скінчених популяцій, що
утворюються за допомогою
скінчених популяцій, що
утворюються за допомогою ![]() перестановок
деякого набору чисел
перестановок
деякого набору чисел ![]() . Тоді в
середньому по всім цим скінченим популяціям
. Тоді в
середньому по всім цим скінченим популяціям
![]() .
.
Зауважимо, що ![]() для усіх перестановок
однакова.
для усіх перестановок
однакова.
Ця теорема стверджує, що якщо
перестановку, яка визначає порядок значень у деякій конкретній скінченій популяції,
можна вважати обраною навмання із можливих ![]() перестановок,
то в середньому систематичний відбір еквівалентний простому випадковому
відбору.
перестановок,
то в середньому систематичний відбір еквівалентний простому випадковому
відбору.
При іншому підході скінчену популяцію вважають добутою навмання з деякої нескінченої надпопуляції, що має певн властивості. Теорема 1.3.1 відноситься не до будь-якої скінченої популяції, а до середнього по всім скінченим популяціям, які можуть бути добуті із дано нескінченої надпопуляції.
Позначимо через ![]() - середнє по всім скінченним
популяціям, які можуть бути добуті з даної надпопуляції.
- середнє по всім скінченним
популяціям, які можуть бути добуті з даної надпопуляції.
Теорема 1.3.2. Якщо змінні ![]()
![]() добуті за допомогою
випадкового відбору із надпопуляції, для якої
добуті за допомогою
випадкового відбору із надпопуляції, для якої
![]()
![]()
![]() ,
, ![]() ,
,
![]() .
.
Головну роль відіграють дв умови:
1)
всі ![]() мають одне і теж середнє
мають одне і теж середнє ![]() , тобто в їх змінах
відсутній будь-який тренд;
, тобто в їх змінах
відсутній будь-який тренд;
2)
між
значеннями ![]() та
та ![]() у двох різних точках
відсутня лінійна кореляція. Дисперсія
у двох різних точках
відсутня лінійна кореляція. Дисперсія ![]() може
бути різною для різних
може
бути різною для різних ![]() .
.
Доведення. Для будь-якої визначеної скінченої популяції
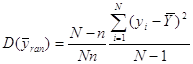 .
.
Далі,
![]()
![]()
![]()
![]()
![]() .
.
Оскільки ![]() та
та ![]() некорельовані
некорельовані ![]() , то
, то
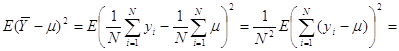
![]() .
.
Отже,
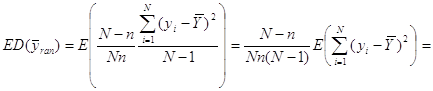
![]()
![]() .
.
Звідси
![]() .
.
Повертаючись до ![]() позначимо через
позначимо через ![]() середнє значення ознаки
для
середнє значення ознаки
для ![]() -тої систематичної вибірки.
Для будь-якої визначеної скінченої популяції
-тої систематичної вибірки.
Для будь-якої визначеної скінченої популяції
![]()
![]()
![]()
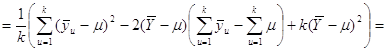
![]()
![]() .
.
За теоремою про дисперсію середнього для некорельованої вибірки, добутої з нескінченої популяції
![]() ~
~![]() ,
,
![]() ,
,
![]() .
.
Розглянемо докладніше вираз у дужках
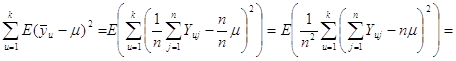
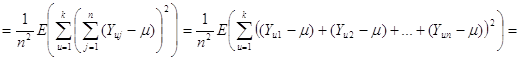
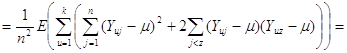
![]() .
.
Раніше було показано, що
![]() .
.
Отже маємо
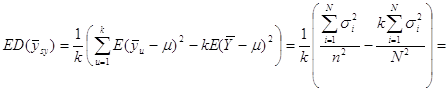
![]()
![]() .
.
Теорема доведена.
1.4 Популяції з лінійним трендом
Якщо популяція містить тільки
лінійний тренд, як показано на рис.1.4.1, то характер результатів уявити собі досить
просто. З рис. 1.4.1 видно, що ![]() та
та ![]() (при вибірці з однією
одиницею із кожної страти) будуть менше, ніж
(при вибірці з однією
одиницею із кожної страти) будуть менше, ніж ![]() .
Крім того,
.
Крім того, ![]() буде більше, ніж
буде більше, ніж ![]() , оскільки, якщо в деякій
страті значення спостереження менше середнього для цієї страти, то при
систематичному відборі значення спостереження буде менше в усіх інших стратах,
в той час, як при випадковому стратифікованому відборі помилки всередині страт
можуть взаємно знищуватись.
, оскільки, якщо в деякій
страті значення спостереження менше середнього для цієї страти, то при
систематичному відборі значення спостереження буде менше в усіх інших стратах,
в той час, як при випадковому стратифікованому відборі помилки всередині страт
можуть взаємно знищуватись.
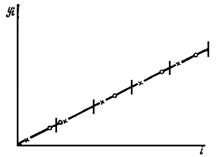
Рис. 1.4.1. Систематичний
відбір із популяцій з лінійним трендом: ![]() -
систематична вибірка,
-
систематична вибірка, ![]() -
стратифікована вибірка
-
стратифікована вибірка
Для теоретичної перевірки цих
результатів достатньо розглянути випадок, коли ![]() ,
,
![]() . Маємо
. Маємо
![]() ;
; ![]() ;
; ![]() . (1.4.1)
. (1.4.1)
Дисперсія сукупності, ![]() , дорівнює:
, дорівнює:
![]() . (1.4.2)
. (1.4.2)
Отже, дисперсія середнього ![]() для простої випадково
вибірки дорівнює:
для простої випадково
вибірки дорівнює:
![]() . (1.4.3)
. (1.4.3)
Для того, щоб знайти
дисперсію всередині страт, ![]() ,
достатньо лише підставити у формулу (1.4.2)
,
достатньо лише підставити у формулу (1.4.2) ![]() замість
замість
![]() . Це дає
. Це дає
![]() (1.4.4)
(1.4.4)
![]()
При систематичному відбор
середнє значення для другої вибірки перевищує середнє для першої на 1; середнє значення
для третьої вибірки перевищує середнє для другої на 1 і т.д. Тому при
обчисленні дисперсії середні ![]() можна
замінити числами
можна
замінити числами ![]() . Отже, виходячи
з (1.4.2), використовуючи
. Отже, виходячи
з (1.4.2), використовуючи
![]() ;
; ![]() ,
,
Отримаємо
![]()
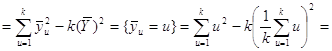
![]()
![]() .
.
Звідси
![]() . (1.4.5)
. (1.4.5)
З формул (1.4.3), (1.4.4), (1.4.5) випливає, що
![]() .
.
Дисперсії для різних способів
відбору рівні тільки при ![]() . Таким
чином, якщо ми хочемо уникнути впливу лінійного тренду (очікуваного або
неочікуваного), то для цієї мети систематична вибірка набагато ефективніша, ніж
проста випадкова вибірка, але менш ефективна, ніж стратифікована випадкова
вибірка.
. Таким
чином, якщо ми хочемо уникнути впливу лінійного тренду (очікуваного або
неочікуваного), то для цієї мети систематична вибірка набагато ефективніша, ніж
проста випадкова вибірка, але менш ефективна, ніж стратифікована випадкова
вибірка.
Ефект використання систематичного
відбору за наявності лінійного тренду можна збільшити кількома способами. Один
з них полягає у тому, щоб використати центрально розташовану вибірку. Інший −
в тому, щоб при обчисленні оцінки замість незваженого середнього брати зважене,
в якому усім внутрішнім членам вибірки надається вага, що дорівнює одиниці (до
ділення на ![]() ), а першому та останньому
членам − інша вага. Якщо число, яке відібране навмання з чисел
), а першому та останньому
членам − інша вага. Якщо число, яке відібране навмання з чисел ![]() виявиться рівним
виявиться рівним ![]() , то ця вага буде
дорівнювати
, то ця вага буде
дорівнювати
![]() ,
,
причому вага, що надається
першому члену, має знак «+», а останньому − знак «-». Очевидно, що при
будь-якому ![]() сума цих двох ваг дорівню
2.
сума цих двох ваг дорівню
2.
1.5 Популяції з періодичною варіацією
Якщо популяція містить
періодичний тренд, наприклад, звичайну синусоїду, то ефективність систематично
вибірки залежить від значення ![]() . Це
можна наочно побачити на рис. 1.5.1. Висота кривої на ньому відповіда
спостереженню
. Це
можна наочно побачити на рис. 1.5.1. Висота кривої на ньому відповіда
спостереженню ![]() .
.
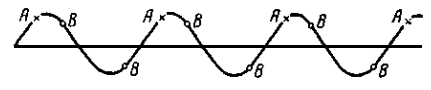
Рис.1.5.1. Періодична варіація
Вибіркові точки ![]() представляють найменш
сприятливий для систематичної вибірки випадок. Він має місце, якщо
представляють найменш
сприятливий для систематичної вибірки випадок. Він має місце, якщо ![]() дорівнює періоду синусоїди
або цілому числу, яке кратне цьому періоду. Кожне спостереження в систематичній
вибірці буде однаковим, тому вибірка не буде більш точною, ніж одиничне
спостереження, добуте з популяції навмання.
дорівнює періоду синусоїди
або цілому числу, яке кратне цьому періоду. Кожне спостереження в систематичній
вибірці буде однаковим, тому вибірка не буде більш точною, ніж одиничне
спостереження, добуте з популяції навмання.
Найбільш сприятливим буде
випадок (вибірка ![]() ), коли
), коли ![]() - непарне число, яке
кратне напівперіоду. Середнє значення кожної систематичної вибірки буде в
точності дорівнювати середньому для популяції, оскільки відхилення вверх або
вниз від прямої на рис. 1.5.1 взаємно урівноважаться. Отже, дисперсія
середнього вибірки буде дорівнювати нулю. У проміжках між цими двома випадками
ефективність вибірки буде залежати від співвідношення між
- непарне число, яке
кратне напівперіоду. Середнє значення кожної систематичної вибірки буде в
точності дорівнювати середньому для популяції, оскільки відхилення вверх або
вниз від прямої на рис. 1.5.1 взаємно урівноважаться. Отже, дисперсія
середнього вибірки буде дорівнювати нулю. У проміжках між цими двома випадками
ефективність вибірки буде залежати від співвідношення між ![]() та довжиною хвилі.
та довжиною хвилі.
Популяції, які можна описати точною синусоїдою, на практиці, не зустрічаються. Однак популяції з більш або менш вираженим періодичним трендом − не рідкість. Прикладами можуть бути транспортний потік на певній ділянці дороги на протязі доби та об’єм продаж у магазині на протязі семи днів тижня. Для оцінювання середнього за деякий період часу було б, очевидно, не доцільно формувати систематичну вибірку, роблячи спостереження щоденно о 4 годині дня кожний четвер. Навпроти, потрібно розосереджувати вибірку вздовж періодичної кривої, у випадку продаж, наприклад, слідкуючи за тим, щоб кожний день тижня був однаково представлений у вибірці.
У деяких популяціях зустрічаються менш помітні періодичні коливання. Наприклад, якщо є ряд щоденних платіжних відомостей для невеликої ділянки підприємства, то список робітників у кожній з них може бути складений у одному й тому ж порядку та містити від 19 до 23 прізвищ. Тоді систематична вибірка кожного 20-го робітника за період декількох тижнів може включати записи, які відносяться до одного і того ж робітника або до двох чи до трьох робітників, що належать до найбільш високооплачувано групи. Аналогічно систематична вибірка прізвищ з міського довідника, де під однаковим прізвищем, спочатку, значиться голова домогосподарства, а потім його діти, може містити дуже багато голів домогосподарств чи дуже багато дітей. Якщо часу вистачає, щоб дослідити характер періодичності, то систематичну вибірку можна побудувати так, щоб скористатися її особливостями. В супротивному разі, коли періодичність передбачається, але характер її невідомий, краще застосовувати просту або стратифіковану випадкову вибірку.
1.6 Автокорельовані популяції
Для багатьох реальних популяцій
підстави очікувати, що два спостереження ![]() та
та
![]() будуть більш схожими, якщо
одиниці
будуть більш схожими, якщо
одиниці ![]() та
та ![]() розташовані в ряд
недалеко одна від одної. Таке буває, коли будь-які природні причини обумовлюють
повільну зміну значень при просуванні вздовж ряду. В математичній моделі тако
ситуації можна вважати, що між
розташовані в ряд
недалеко одна від одної. Таке буває, коли будь-які природні причини обумовлюють
повільну зміну значень при просуванні вздовж ряду. В математичній моделі тако
ситуації можна вважати, що між ![]() та
та ![]() існує додатна кореляція,
яка залежить тільки від відстані між ними,
існує додатна кореляція,
яка залежить тільки від відстані між ними, ![]() ,
та прямує до нуля при збільшенні цієї відстані.
,
та прямує до нуля при збільшенні цієї відстані.
Для з’ясування того, чи можна
застосовувати цю модель до конкретної популяції, можна обчислити коефіцієнти
кореляції ![]() між парами спостережень,
що знаходяться на відстані
між парами спостережень,
що знаходяться на відстані ![]() одиниць
одне від одного, та побудувати графік відповідних значень як функції
одиниць
одне від одного, та побудувати графік відповідних значень як функції ![]() . Цей графік, чи функція,
яку він представляє, називається корелограмою. Навіть якщо модель можна
застосовувати до будь-якої скінченої популяції, корелограма для неї не буде
гладкою функцією через неправильності, обумовлені скінченим характером популяції.
При порівнянні систематичного та стратифікованого випадкового відборів із популяцій,
що описуються моделлю, ці неправильності ускладнюють отримання результатів для
будь-якої скінченої популяції. Таке порівняння можна провести, якщо розглядати
середнє з цілого ряду популяцій, отриманих навмання з деякої нескінченої надпопуляції,
до якої можна застосувати цю модель. Такий прийом вже застосовувався в теорем
1.3.2.
. Цей графік, чи функція,
яку він представляє, називається корелограмою. Навіть якщо модель можна
застосовувати до будь-якої скінченої популяції, корелограма для неї не буде
гладкою функцією через неправильності, обумовлені скінченим характером популяції.
При порівнянні систематичного та стратифікованого випадкового відборів із популяцій,
що описуються моделлю, ці неправильності ускладнюють отримання результатів для
будь-якої скінченої популяції. Таке порівняння можна провести, якщо розглядати
середнє з цілого ряду популяцій, отриманих навмання з деякої нескінченої надпопуляції,
до якої можна застосувати цю модель. Такий прийом вже застосовувався в теорем
1.3.2.
Отже, ми припускаємо, що
спостереження ![]()
![]() вилучені з над популяції,
для якої
вилучені з над популяції,
для якої
![]()
![]()
![]() (1.6.1)
(1.6.1)
де
![]() при довільних
при довільних ![]() .
.
Здобуття одного набору
значень ![]() з цієї надпопуляції призводить
до утворення деякої скінченої популяції обсягом
з цієї надпопуляції призводить
до утворення деякої скінченої популяції обсягом ![]() .
.
Середня дисперсія по всім скінченим популяціям при систематичному відборі позначається через
![]() .
.
Для цього класу популяцій
неважко показати, що стратифікований випадковий відбір краще простого
випадкового відбору, але відносно систематичного відбору загального твердження
сформулювати не можна. Всередині цього класу існують надпопуляції, для яких
систематичний відбір краще стратифікованого випадкового відбору, але існують
такі, для яких, при певних значеннях ![]() ,
систематичний відбір поступається стратифікованому випадковому відбору.
,
систематичний відбір поступається стратифікованому випадковому відбору.
Якщо припустити, що корелограма є випуклою вниз функцією, то можна довести одну загальну теорему.
Теорема 1.6.1. Якщо, разом з умовами (1.6.1), виконується
![]() ,
, ![]() ,
,
то при будь якому обсяз вибірки
![]() .
.
Далі, за винятком випадку ![]()
![]() , виконується
, виконується
![]() .
.
Теорема 1.6.1 була доведена Кокреном у 1946 році.
Наведемо частину доведення
при ![]() , яка показує, яку роль
відіграє умова випуклості вгору. Члени пари, які утворюють систематичну
вибірку, завжди відстоять один від одного на
, яка показує, яку роль
відіграє умова випуклості вгору. Члени пари, які утворюють систематичну
вибірку, завжди відстоять один від одного на ![]() одиниць.
Отже,
одиниць.
Отже,
![]() .
.
У випадку стратифіковано
вибірки для кожної одиниці, що вилучається з відповідної страти, існує ![]() можливих місць, що
утворюють
можливих місць, що
утворюють ![]() можливих комбінацій
розташування вибірки. Числа комбінацій, для яких відстань між одиницями склада
можливих комбінацій
розташування вибірки. Числа комбінацій, для яких відстань між одиницями склада
![]() , будуть такими:
, будуть такими:
| Відстань |
|
Підсумок |
| Число комбінацій |
|
|
Отже, середнє значення ![]() , яке береться по всім
, яке береться по всім ![]() комбінаціям, може бути
подане у вигляді
комбінаціям, може бути
подане у вигляді
![]()
Аналогічно ![]() можна виразити у вигляді
можна виразити у вигляді
![]()
Отже,
![]()
Якщо
![]()
![]() ,
,
то неважко показати, що кожний член всередині дужок додатний. Теорема доведена.
Середня відстань між одиницями
дорівнює ![]() як для систематично
вибірки, так і для стратифікованої вибірки, але завдяки умові випуклост
стратифікована вибірка більш програє у точності, коли відстань між одиницями
менше
як для систематично
вибірки, так і для стратифікованої вибірки, але завдяки умові випуклост
стратифікована вибірка більш програє у точності, коли відстань між одиницями
менше ![]() , ніж виграє, коли ця
відстань більше
, ніж виграє, коли ця
відстань більше ![]() .
.
В 1949 році Кенуй показав, що нерівності, які містяться у твердженні теореми 1.6.1, залишаються справедливими, якщо зробити менш жорсткими дві умови (1.6.1), а саме
![]()
![]() .
.
В цьому випадку кожна з трьох середніх дисперсій для надпопуляції збільшується в однаковому ступені.
1.7 Реальні популяції
Дослідження були проведен для різних реальних популяцій. Деякі з цих досліджень наведені в таблиці 1.7.1. Перші три дослідження проводилися за допомогою географічних мап. У першому з них популяція складається з 288 значень висот точок, які знаходяться на відстані 0,1 милі одна від одної у гірській місцевості.
У двох наступних популяціях даними долі довжин відрізків прямих, які проведені на мапі з розфарбуванням, що приходяться на області з визначеним покриттям (під травою, лісом і т.п.). Ц приклади можна вважати найбільш близькими до моделей з неперервною у строгому сенсі варіацією.
Наступні три дослідження заснован на показах температури на протязі 192 послідовних днів у наступних точках: (а) 12 дюймів під поверхнею трави, (б) 4 дюйма під поверхнею землі, (в) у повітрі. Ці три дослідження відображають три різних ступені впливу (у напрямку збільшення) на характеристику, що вивчаються, а саме - нестійкі щоденні зміни погоди та повільні сезонні зміни.
У останніх дослідженнях спостерігались рослини або дерева, що ростуть у послідовних точках, які розташован вздовж деякої лінії. При обстеженні картоплі, типовою для цієї групи, скінчена популяція складається зі значень врожаю на 96 грядках деякого поля.
У деяких обстеженнях ![]() порівнювали з
порівнювали з ![]() для стратифікованої випадково
вибірки з об’ємом страт
для стратифікованої випадково
вибірки з об’ємом страт ![]() і двома
одиницями у кожній страті. Таке порівняння є цікавим, оскільки за даними
вибірки можна дістати незміщену оцінку
і двома
одиницями у кожній страті. Таке порівняння є цікавим, оскільки за даними
вибірки можна дістати незміщену оцінку ![]() .
Для
.
Для ![]() (з об’ємом страти
(з об’ємом страти ![]() і однією одиницею у кожній
страті) або для
і однією одиницею у кожній
страті) або для ![]() її отримати
неможна. У більшості джерел безпосереднє порівняння з
її отримати
неможна. У більшості джерел безпосереднє порівняння з ![]() у явному вигляді не
проводиться, але взагалі
у явному вигляді не
проводиться, але взагалі ![]() да
виграш у точності у порівнянні з
да
виграш у точності у порівнянні з ![]() .
.
У роботах Йетса та Фінн
порівняння проводиться відносно цілої низки значень ![]() та
та
![]() для кожної скінченої популяції.
для кожної скінченої популяції.
Таблиця 1.7.1 Реальні популяції, що вивчені при аналізі систематичного відбору
| Автор |
Обсяг популяції
|
Вид даних |
| Yates (1948) | 288 | Значення висот у точках, що знаходяться на відстані 0,1 милі одна від одної, отримані за мапою англійського державного картографічного управління |
| Osborne (1942) | * | Відсоток площі під (а) оброблюваною землею, (б) чагарником, (в) травою, (г) лісом на паралельних прямих, які проведені на мапі з розфарбуванням |
| Osborne (1942) | * | Відсоток площі під ялиною Дугласа, який підрахований за допомогою паралельних прямих, що проведені на мапі з розфарбуванням |
| Yates (1948) | 192 | Температура рунту (12 дюймів під поверхнею трави) на протязі 192 послідовних днів |
| Yates (1948) | 192 | Температура рунту (4 дюймів під поверхнею землі) на протязі 192 послідовних днів |
| Yates (1948) | 192 | Температура повітря на протязі 192 послідовних днів |
| Yates (1948) | 96 | Врожай картопл на 96 грядках |
| Finney (1948) | 160 | Об’єм лісу, придатного до продажу, у розрахунку на ділянку шириною у 3 ряди та змінно довжини (Mt. Stuart forest) |
| Finney (1948) | 288 | Об’єм підростаючого лісу на ділянку шириною у 2,5 ряди та довжиною у 80 рядів (Black’s Mountain forest) |
| Finney (1950) | 292 | Об’єм лісу на ділянку шириною в 2 ряди та змінної довжини (Dehra Dun forest) |
| Johnson (1943) | 400** | Число саджанців на 1 фут довжини гряди для 4 гряд саджанців листяних порід |
| Johnson (1943) | 400** | Число саджанців на 1 фут довжини гряди для 3 гряд саджанців хвойних порід |
| Johnson (1943) | 400** | Число пересаджених дерев хвойних порід на 1 фут довжини гряди для 6 гряд |
* Теоретично ![]() нескінчене, якщо вважати,
що товщина прямих нескінченно мала
нескінчене, якщо вважати,
що товщина прямих нескінченно мала
** Наближено. Насправді це число змінювалось від гряди до гряди.
Для цих випадків дані таблиц
1.7.2 є геометричним середнім відношень дисперсій для окремих значень ![]() . Інші автори проводили
порівняння тільки для одного значення
. Інші автори проводили
порівняння тільки для одного значення ![]() у
кожній популяції, але іноді приводили данні для різних ознак або декількох
реальних популяцій одного і того ж характеру. При цьому знову бралось
геометричне середнє з відношень дисперсій.
у
кожній популяції, але іноді приводили данні для різних ознак або декількох
реальних популяцій одного і того ж характеру. При цьому знову бралось
геометричне середнє з відношень дисперсій.
Таблиця 1.7.2 Відносна точність систематичного та стратифікованого випадкового відбору
| Данні |
Розмах значень
|
Відносна точність систематичного відбору в порівнянні зі стратифікованим відбором | |
|
|
|
||
| Висоти | 2 − 20 | 2,99 | 5,68 |
|
Відсоток площі (4 типів покриття) |
− | − | 4,42 |
| Відсоток площі під ялиною Дугласа | − | − | 1,83 |
| Температура рунту (12 дюймів) | 2 − 24 | 2,42 | 4,23 |
| Температура рунту (4 дюйма) | 4 − 24 | 1,45 | 2,07 |
| Температура повітря | 4 − 24 | 1,26 | 1,65 |
| Картопля | 3 − 16 | 1,37 | 1,90 |
| Об’єм лісу (Mt. Stuart) | 2 − 32 | 1,07 | 1,35 |
|
Об’єм лісу (Black’s Mt) |
2 − 24 | 1,19 | 1,44 |
|
Об’єм лісу (Dehra Dun) |
2 − 32 | 1,39 | 1,89 |
| Листян саджанці | 14 | − | 1,89 |
| Хвойн саджанці | 14 − 24 | − | 2,22 |
| Пересадженн хвойні дерева | 12 − 22 | − | 0,93 |
Хоча ці данні обмежені за
масштабами, результати справляють враження. В тих дослідженнях, де можливе
порівняння з ![]() , систематична вибірка
незмінно дає, хоча і помірний, але цілком відчутний виграш у точності. Медіанне
значення відношень
, систематична вибірка
незмінно дає, хоча і помірний, але цілком відчутний виграш у точності. Медіанне
значення відношень ![]() дорівнює 1,4.
Виграш у точності у порівнянні з
дорівнює 1,4.
Виграш у точності у порівнянні з ![]() суттєвіший,
тут медіанне значення відношень дорівнює 1,9. Характер знайдених результатів взагал
відповідає очікуваному, хоча зважаючи на невелику кількість обстежень важко
було розраховувати на отримання певних висновків. Виграш виявився найбільшим
для тих видів даних, відносно яких можна було припустити, що їхня варіація
найбільш близька до неперервної. З цієї точки зору і при переході від ґрунтових
температур до температур повітря можна було очікувати, що відношення
суттєвіший,
тут медіанне значення відношень дорівнює 1,9. Характер знайдених результатів взагал
відповідає очікуваному, хоча зважаючи на невелику кількість обстежень важко
було розраховувати на отримання певних висновків. Виграш виявився найбільшим
для тих видів даних, відносно яких можна було припустити, що їхня варіація
найбільш близька до неперервної. З цієї точки зору і при переході від ґрунтових
температур до температур повітря можна було очікувати, що відношення ![]() зменшиться. З останніх
трьох ознак (дані про лісові розсадники) виграшу у точності не виявилось лише
для одного − пересаджених хвойних дерев
зменшиться. З останніх
трьох ознак (дані про лісові розсадники) виграшу у точності не виявилось лише
для одного − пересаджених хвойних дерев ![]() ,
які старіші й більш однорідні, ніж молоді саджанці.
,
які старіші й більш однорідні, ніж молоді саджанці.
1.8 Оцінювання дисперсії за окремою вибіркою
Згідно з результатами, як
відносяться до простих випадкових вибірок з ![]() ,
ми можемо обчислити незміщену оцінку дисперсії вибіркового середнього, при цьому
оцінка буде незміщеною незалежно від виду популяції. Але для систематично
вибірки ця корисна властивість не зберігається, оскільки її можна розглядати
лише як просту випадкову вибірку з
,
ми можемо обчислити незміщену оцінку дисперсії вибіркового середнього, при цьому
оцінка буде незміщеною незалежно від виду популяції. Але для систематично
вибірки ця корисна властивість не зберігається, оскільки її можна розглядати
лише як просту випадкову вибірку з ![]() , тобто
одним членом. Проілюструємо це на прикладі зі зміною «по синусоїді». Нехай
, тобто
одним членом. Проілюструємо це на прикладі зі зміною «по синусоїді». Нехай
![]() ,
,
де ![]() (обираємо кожну четверту
одиницю) та
(обираємо кожну четверту
одиницю) та ![]() Послідовними спостереженнями
в популяції будуть
Послідовними спостереженнями
в популяції будуть
![]()
Якщо за перший член обрати
значення ![]() , то всі члени
систематичної вибірки мають значення
, то всі члени
систематичної вибірки мають значення ![]() . При
трьох інших можливих значеннях першого члена всі вони приймають значення
відповідно
. При
трьох інших можливих значеннях першого члена всі вони приймають значення
відповідно ![]() ,
, ![]() або
або ![]() . Таким чином, за окремою
вибіркою ми не можемо оцінити величину
. Таким чином, за окремою
вибіркою ми не можемо оцінити величину ![]() .
В той час справжнє значення дисперсії вибіркового середнього систематично
вибірки дорівнює
.
В той час справжнє значення дисперсії вибіркового середнього систематично
вибірки дорівнює ![]() . Цей приклад ілюструє,
що при існуванні періодичної варіації в популяції незміщену оцінку дисперсії по
вибірці побудувати неможливо.
. Цей приклад ілюструє,
що при існуванні періодичної варіації в популяції незміщену оцінку дисперсії по
вибірці побудувати неможливо.
Але останнє не означає, що зовсім нічого не можна зробити. За виключенням випадку періодичної варіації, ми можемо користуватися інформацією про структуру популяції для того, щоб побудувати математичну модель, яка адекватно представляє існуючий в популяц тип варіації. Після цього ми могли б вивести формулу для оцінки дисперсії, яка для цієї моделі була б наближено незміщеною, хоча, можливо, для інших моделей зміщення було б великим. Вирішувати, яку з моделей необхідно застосовувати, повинен той, хто організовує спостереження.
Далі наведені без доведень деяк прості моделі з відповідними оцінками дисперсій.
Найбільш проста модель відноситься
до популяції, в якій ![]() містить деякий
тренд плюс «випадковий» доданок. Тоді
містить деякий
тренд плюс «випадковий» доданок. Тоді
![]() ,
,
де ![]() − деяка функція
− деяка функція ![]() . Відносно випадкового
доданка
. Відносно випадкового
доданка ![]() ми припускаємо, що існує надпопуляція,
для якої
ми припускаємо, що існує надпопуляція,
для якої
![]()
![]()
![]()
![]() .
.
Оцінка дисперсії ![]() називається незміщеною
оцінкою дисперсії
називається незміщеною
оцінкою дисперсії ![]() , якщо
, якщо
![]() ,
,
тобто, якщо вона незміщена відносно середнього по всім скінченим популяціям, які можуть бути отримані з цієї надпопуляції.
Популяція, одиниці яко розташовані навмання.
![]()
![]()
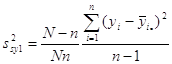 .
.
Остання формула є оцінкою
дисперсії систематичної вибірки ![]() - то
одиниці.
- то
одиниці.
Ця модель застосовується, якщо ми впевненні в тому, що порядок розташування одиниць має в основному випадковий характер відносно ознаки, що спостерігається. Формула дисперсії збігається з формулою дисперсії простого випадкового відбору, і її оцінка незміщена, якщо наша модель справедлива.
Стратифікована популяція, одиниці якої у стратах розташовані навмання
![]()
![]()
![]() .
.
В цьому випадку середн
значення є постійним всередині кожної страти з ![]() одиниць.
Оцінка
одиниць.
Оцінка ![]() , яка заснована на
середньому квадраті послідовних різниць, не буде незміщеною. В її утворенн
приймають небажану участь різниці значень
, яка заснована на
середньому квадраті послідовних різниць, не буде незміщеною. В її утворенн
приймають небажану участь різниці значень ![]() сусідніх
страт і, зокрема, при оцінюванні випадкового доданку дисперсії перша та остання
страти мають занадто малу вагу. Якщо наша модель справедлива, то для достатньо
великих вибірок ця оцінка буде, взагалі кажучи, перевищувати дисперсію.
сусідніх
страт і, зокрема, при оцінюванні випадкового доданку дисперсії перша та остання
страти мають занадто малу вагу. Якщо наша модель справедлива, то для достатньо
великих вибірок ця оцінка буде, взагалі кажучи, перевищувати дисперсію.
Лінійний тренд
![]()
![]()
![]() .
.
Оцінка заснована на квадратах
послідовних різниць, що утворюються трьома сусідніми значеннями ![]() ,
, ![]() ,
, ![]() у вибірці. Сума квадратів
містить
у вибірці. Сума квадратів
містить ![]() членів. У випадку
лінійного тренду його можна виключити, використовуючи кінцеві поправки. Член
членів. У випадку
лінійного тренду його можна виключити, використовуючи кінцеві поправки. Член ![]() дорівнює сумі квадратів
ваг у виразі
дорівнює сумі квадратів
ваг у виразі ![]() . Якщо тільки
. Якщо тільки ![]() не мале,
не мале, ![]() можна замінити звичайним
множником
можна замінити звичайним
множником ![]() . Це можна зробити,
оскільки крайнім стратам надана дуже мала вага, оцінка зміщена, за виключенням
випадку, коли
. Це можна зробити,
оскільки крайнім стратам надана дуже мала вага, оцінка зміщена, за виключенням
випадку, коли ![]() є постійною
величиною. Але якщо
є постійною
величиною. Але якщо ![]() велике і наша
модель справедлива, то оцінка буде цілком задовільною.
велике і наша
модель справедлива, то оцінка буде цілком задовільною.
1.9 Стратифікований систематичний відбір
Якщо одиниці певним чином впорядковані, то систематичний відбір забезпечує деякого роду стратифікування з рівними долями відбору. Якщо стратифікування виконано за деяким іншим критерієм, то з кожної страти можна вилучити окрему систематичну вибірку, визначаючи точки відліку незалежно. Такий підхід зручний, якщо ми хочемо отримати окремі оцінки для кожної страти або якщо застосовуються нерівні дол відбору. Цей метод буде, звичайно, більш точним, ніж стратифікований випадковий відбір, якщо систематичний відбір всередині страт більш точний, ніж випадковий відбір всередині страт.
Якщо ![]() − середнє значення
для систематичної вибірки у страті
− середнє значення
для систематичної вибірки у страті ![]() , то
оцінка середнього для сукупності
, то
оцінка середнього для сукупності ![]() дисперсія мають вигляд:
дисперсія мають вигляд:
![]()
![]() .
.
Якщо страт небагато, то
задача знаходження дисперсії за вибіркою зводиться до задачі пошуку за вибіркою
задовільної оцінки ![]() у кожній страті.
у кожній страті.
Якщо страт багато, то може бути кращою оцінка, знайдена за методом «поєднанних страт». Оцінка
![]() ,
,
де підсумовування проводиться за всіма парами страт, у середньому перебільшує дисперсію, навіть якщо варіація періодичного характеру існує всередині страт.
Незміщену оцінку дисперс
похибки можна отримати, якщо з кожної страти вилучаються дві систематичн
вибірки з різними точками відліку, які обрані навмання, та з інтервалом відбору
![]() . При цьому кожна страта
забезпечує один ступінь вільності. Якщо систематичний відбір є ефективним, то
такий прийом призведе до деякої втрати точності. Якщо страт багато, то з
більшості їх можна добути по одній систематичній вибірці, а по дві вибірки для
оцінювання по ним похибки вилучити лише у частині страт, відібравши цю частину навмання.
. При цьому кожна страта
забезпечує один ступінь вільності. Якщо систематичний відбір є ефективним, то
такий прийом призведе до деякої втрати точності. Якщо страт багато, то з
більшості їх можна добути по одній систематичній вибірці, а по дві вибірки для
оцінювання по ним похибки вилучити лише у частині страт, відібравши цю частину навмання.
1.10 Двовимірний систематичний відбір
При відборі з популяції, що представля собою деяку територію, найпростішим узагальненням одновимірного систематичного відбору буде відбір за схемою квадратної решітки, яка зображена на рис.1.10.1. Вибірка повністю визначається парою випадкових чисел, які задають координати лівої верхньої одиниці.
Характеристики схеми
квадратної решітки були дослідженні на прикладах як теоретичних, так і реальних
популяцій. Матерн (1960) дослідив найкращий тип вибірки для випадку, коли
кореляція спостережень у довільних двох точках виражається монотонно спадаючою
випуклою вгору функцією відстані між ними ![]() .
Для корелограм вигляду
.
Для корелограм вигляду ![]() відбір по
квадратній решітці виявляється достатньо придатним і перевищує простий або
стратифікований випадковий відбір з однією одиницею у кожній страті, хоча
Матерн і вказує причини, за якими можна очікувати, що найкращою схемою для ц
ситуації виявиться відбір по трикутній решітці, що утворені вершинами
рівносторонніх трикутників.
відбір по
квадратній решітці виявляється достатньо придатним і перевищує простий або
стратифікований випадковий відбір з однією одиницею у кожній страті, хоча
Матерн і вказує причини, за якими можна очікувати, що найкращою схемою для ц
ситуації виявиться відбір по трикутній решітці, що утворені вершинами
рівносторонніх трикутників.
У 14 сільськогосподарських дослідженнях на однорідність Хейнс (1948) знайшов, що відбір за квадратною решіткою дає майже ту саму точність, що і двовимірний простий випадковий відбір. Мілн (1959) вивчав відбір за «центральною» схемою квадратної решітки, коли вибірка визначається точкою, яка лежить в центрі квадрату, у 50 випробуваннях на однорідність. Такий спосіб відбору виявився краще простого випадкового відбору , можливо, дещо краще, ніж стратифікований випадковий відбір, хоча остання перевага не була статистично значущою. Ці результати вказують на те, що принаймні, для даних такого типу, автокореляція виражена слабко. При оцінюванні по мапі площі, яку займа ліс чи вода, Матерн у двох прикладах помітив, що квадратна решітка перевищу випадкові методи відбору.
Два типи двовимірної систематичної вибірки
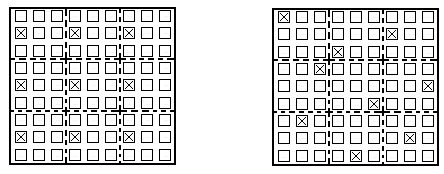
Рис. 1.10.1 Рис. 1.10.2 Вирівняна вибірка або Невирівняна вибірка за схемою «квадратної решітки»
На рис. 1.10.2 наведена систематична вибірка іншого типу, яка називається невирівняною вибіркою.
1. Добуваючи пару випадкових чисел, задаємо координати ліво верхньої одиниці:
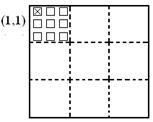
2. Добуваючи пару випадкових чисел, задаємо горизонтальн координати двох одиниць в першому стовбці:
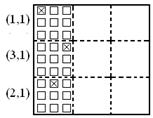
Наприклад, в другому рядку − координати правої одиниці, в третьому рядку − координати центральної одиниці.
3. Добуваючи пару випадкових чисел, задаємо вертикальн координати двох одиниць в першому рядку:
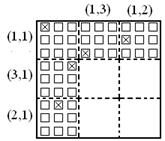
Наприклад, в другому стовбці − координати нижньо одиниці, в третьому стовбці − координати центральної одиниці.
Після цього постійний інтервал ![]() (що
дорівнює сторонам квадратів) однозначно задає розташування всіх інших точок. Дослідження
Кенуя (1949) і Даса (1950) для простих двовимірних корелограм вказують на те,
що невирівняна схема часто дає кращі результати, ніж квадратна решітка та
стратифікований випадковий відбір.
(що
дорівнює сторонам квадратів) однозначно задає розташування всіх інших точок. Дослідження
Кенуя (1949) і Даса (1950) для простих двовимірних корелограм вказують на те,
що невирівняна схема часто дає кращі результати, ніж квадратна решітка та
стратифікований випадковий відбір.
Ще одне свідчення переваги невирівняної вибірки дає досвід
планування експериментів, який виявив, що для розміщення спостережень у
прямокутній області цілком можна застосовувати схему латинського квадрату. Вважатимемо,
що латинський квадрат (5![]() 5), який
показаний на рис. 1.10.3, задає розбиття області на п’ять систематичних
вибірок, кожна з яких відповідає певній літері. Є деякі данні про те, що цей
особливий квадрат, що називається латинським квадратом «ходом коня», буде більш
точним, ніж навмання вибраний квадрат (5
5), який
показаний на рис. 1.10.3, задає розбиття області на п’ять систематичних
вибірок, кожна з яких відповідає певній літері. Є деякі данні про те, що цей
особливий квадрат, що називається латинським квадратом «ходом коня», буде більш
точним, ніж навмання вибраний квадрат (5![]() 5).
Причина цього, ймовірно, у тому, що у першого ніяка вибірка не містить двох
елементів не тільки з одного рядка чи одного стовпця, але й із кожно
діагоналі.
5).
Причина цього, ймовірно, у тому, що у першого ніяка вибірка не містить двох
елементів не тільки з одного рядка чи одного стовпця, але й із кожно
діагоналі.
Принципом побудови латинських квадратів скористалися Хомейер та Блек при відборі на прямокутних полях вівса. Кожне поле містило 21 ділянку. Три можливі систематичні вибірки, які позначені відповідно літерами A, B, C, що показані на рис. 1.10.4. Таке розміщення, коли на кожному полі обирається навмання одна з літер, збільшило точність приблизно на 25% у порівнянні з стратифікованим випадковим відбором, в якому рядки виступали стратами. Оскільки кожна літера зустрічається тричі в одному стовпчику і по два рази в інших, таке розміщення не зовсім точно задовольняє означенню латинського квадрату, але, наскільки це можливо, відповідає йому.
Дві схеми систематичного відбору, засновані на латинських квадратах

Рис. 1.10.3 Латинський квадрат «ходом коня» Рис. 1.10.4 Схема
систематичного відбору для прямокутного поля 3![]() 7
7
Йейтс (1960), який назвав розміщення такого типу відбором за
решіткою, розглядає їх застосування для двовимірного та тривимірного відбору. У
випадку трьох вимірів кожний рядок, кожний стовпець та кожна вертикаль можуть
бути представлені у вибірці шляхом відбору ![]() одиниць
з
одиниць
з ![]() одиниць популяції. Якщо
вибірка містить
одиниць популяції. Якщо
вибірка містить ![]() одиниць, то в
ній можуть бути представленні кожне з
одиниць, то в
ній можуть бути представленні кожне з ![]() сполук
рядків та стовпців або рядків та вертикалей, або стовпців та вертикалей.
Паттерсон (1954) дослідив розміщення, які дають незміщену оцінку похибки.
сполук
рядків та стовпців або рядків та вертикалей, або стовпців та вертикалей.
Паттерсон (1954) дослідив розміщення, які дають незміщену оцінку похибки.
1.11 Приклади розв’язування задач
Приклад 1. У таблиц 1.11.1 наведена кількість саджанців на кожному футі довжини гряди, загальною довжиною у 200 футів.
Знайти дисперсію середнього систематичної вибірки, що включа
кожний двадцятий фут гряди. Порівняти її з дисперсією простої випадково
вибірки. Для всіх вибірок ![]() .
. ![]()
Таблиця 1.11.1 Число саджанців
| Фути довжини гряди | Підсумки систематичних вибірок | ||||||||||
| 1-20 | 21-40 | 41-60 | 61-80 | 81-100 | 101-120 | 121-140 | 141-160 | 161-180 | 181-200 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|
8 6 6 23 25 16 28 21 22 18 26 28 11 16 7 22 44 26 31 26 |
20 19 25 11 31 26 29 19 17 28 16 9 22 26 17 39 21 14 40 30 |
26 26 10 41 30 55 34 56 39 41 27 20 25 39 24 25 18 44 55 39 |
34 21 27 25 32 43 33 45 23 27 37 14 14 24 18 17 14 38 36 29 |
31 23 41 18 15 21 8 22 11 3 4 5 11 9 25 16 13 22 18 9 |
24 19 28 18 29 24 33 37 32 26 36 20 43 27 20 21 18 19 24 30 |
18 13 7 9 11 20 16 9 14 15 20 21 15 14 13 9 25 17 7 30 |
16 12 8 10 12 20 17 12 7 17 21 26 16 18 11 19 27 29 31 29 |
36 8 29 33 14 13 18 20 13 24 29 18 16 20 6 15 4 8 8 10 |
10 35 7 9 12 7 6 14 12 15 18 4 4 9 8 8 9 10 5 3 |
223 182 188 197 211 245 222 255 190 214 234 165 177 202 149 191 193 227 225 235 |
|
| Підсумки для страт | 410 | 459 | 674 | 554 | 325 | 528 | 303 | 358 | 342 | 205 | 4155 |
Розв’язання.
а) Систематична вибірка:
![]()
![]()
![]()
Дисперсія середнього систематичної вибірки дорівнює ![]() .
.
б) Проста випадкова вибірка:
![]()
![]()
![]()
Дисперсія простої випадкової вибірки дорівнює ![]() .
.
Відповідь: ![]() . Дисперсія середнього систематичної вибірки краща ніж
дисперсія простої випадкової вибірки.
. Дисперсія середнього систематичної вибірки краща ніж
дисперсія простої випадкової вибірки.
Приклад 2. Популяція, що складається з 360 домогосподарств (які перенумеровані від 1 до 360), розміщена в картотеці у алфавітному порядку за прізвищами головних членів господарств. Домогосподарства, де голова сім’ї небілий, мають наступні номери: 28, 31-33, 36-41, 44, 45, 47, 55, 56, 58, 68, 69, 82, 83, 85, 86, 89-94, 98, 99, 101, 107-110, 114, 154, 156, 178, 223, 224, 296, 298-300, 302-304, 306-323, 325-331, 333, 335-339, 341, 342. (Серед небілих іноді зустрічаються «скупчення» домогосподарств через зв'язок між прізвищем та кольором шкіри).
Порівняйте точність систематичної вибірки кожного восьмого домогосподарства з простою випадковою вибіркою того ж обсягу при оцінюванні частки домогосподарств, у яких головний член сім’ї небілий.
Розв’язання.
Будемо позначати домогосподарство, де голова сім’ї небілий як 1 і відповідно де голова білий 0. Тоді запишемо всі систематичні вибірки кожного восьмого домогосподарства у таблицю 1.11.2:
Таблиця 1.11.2 Дані по 8-ми систематичним вибіркам
|
Номер
систематичної вибірки ( |
||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
|
|
0,2222 | 0,2667 | 0,1556 | 0,2667 | 0,2667 | 0,2222 | 0,2444 | 0,1556 |
|
|
10 | 12 | 7 | 12 | 12 | 10 | 11 | 7 |
а) Систематична вибірка
Середнє значення систематичної вибірки має розподіл
![]() ~
~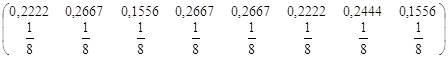
![]()
![]()
![]()
Дисперсія середнього
систематичної вибірки дорівнює ![]() .
.
б) Проста випадкова вибірка
Частка домогосподарств, де головний член сім’ї не білий дорівнює
![]()
Для простої випадково вибірки дисперсія вибіркової частки має вигляд:
![]() ,
,
де ![]() ,
, ![]() . Підставляємо і отримаємо:
. Підставляємо і отримаємо:
![]() .
.
Дисперсія простої випадково
вибірки при оцінюванні частки домогосподарств з небілим головним членом сім
дорівнює ![]() .
.
Відповідь: ![]() . Дисперсія систематично
вибірки точніша за дисперсію простої випадкової вибірки при оцінюванні частки
домогосподарств, де головний член сім’ї небілий.
. Дисперсія систематично
вибірки точніша за дисперсію простої випадкової вибірки при оцінюванні частки
домогосподарств, де головний член сім’ї небілий.
Приклад 3. Є наступний список мешканців 13-ти будинків деякої вулиці. М – дорослий чоловік, Ж – доросла жінка, м хлопчик, ж – дівчинка.
Сім’ї
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| М | М | М | М | М | М | М | М | М | М | М | М | М |
| Ж | Ж | Ж | Ж | Ж | Ж | Ж | Ж | Ж | Ж | Ж | Ж | Ж |
| ж | ж | м | м | ж | ж | м | м | м | ж | ж | ||
| м | м | ж | м | м | ж | ж | ж | м | ||||
| ж | ж | ж | м |
Порівняйте дисперсії для систематичної вибірки кожної п’ятої людини та 20%-вої простої випадково вибірки при оцінюванні: (а)частки людей чоловічої статі, (б) частки дітей. У випадку систематичної вибірки ведіть відлік у кожному стовбці зверху вниз далі з верху наступного стовпця.
Розв’язання.
Запишемо всі систематичн вибірки кожної п’ятої людини:
1. М М М Ж ж М М Ж ж М
2. Ж Ж Ж М М Ж Ж м М Ж
3. ж ж м Ж Ж ж м М Ж ж
4. м м ж м ж ж ж Ж ж М
5. ж ж М м м м М м м Ж
а) Оцінювання частки людей чоловічої статі
· Систематична вибірка кожної п’ятої людини
![]()
![]()
![]()
![]()
![]()
Тоді розподіл середнього ма вигляд:
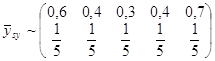 .
.
![]()
![]()
![]()
Дисперсія середнього
систематичної вибірки дорівнює ![]() .
.
· 20%-ва проста випадкова вибірка
Якщо ![]() , тоді
, тоді ![]() . Частка людей чоловічо
статі дорівнює
. Частка людей чоловічо
статі дорівнює
![]()
Тоді дисперсія вибірково частки простої випадкової вибірки дорівнює
![]()
Дисперсія простої випадково
вибірки при оцінюванні частки людей чоловічої статі дорівнює ![]() .
.
б) Оцінювання частки дітей
· Систематична вибірка кожної п’ятої людини
![]()
![]()
![]()
![]()
![]()
Тоді розподіл середнього ма вигляд:
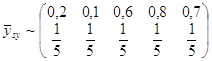 .
.
![]()
![]()
![]()
Дисперсія середнього систематично
вибірки дорівнює ![]() .
.
· 20%-ва проста випадкова вибірка
Якщо ![]() , тоді
, тоді ![]() . Частка дітей дорівнює
. Частка дітей дорівнює
![]()
Тоді дисперсія вибірково частки простої випадкової вибірки дорівнює
![]()
Дисперсія простої випадково
вибірки при оцінюванні частки дітей дорівнює ![]() .
.
Відповідь: а) При оцінюванні частки
людей чоловічої статі отримали, що ![]() .
Дисперсія систематичної вибірки точніша за дисперсію 20%-ї простої випадково
вибірки. Але можна помітити, що вони майже рівні. б) При оцінюванні частки
дітей отримали, що
.
Дисперсія систематичної вибірки точніша за дисперсію 20%-ї простої випадково
вибірки. Але можна помітити, що вони майже рівні. б) При оцінюванні частки
дітей отримали, що ![]() . В цьому випадку
дисперсія 20%-ї простої випадкової вибірки є кращою ніж дисперсія систематично
вибірки.
. В цьому випадку
дисперсія 20%-ї простої випадкової вибірки є кращою ніж дисперсія систематично
вибірки.
РОЗДІЛ ІІ. ПОРІВНЯННЯ СИСТЕМАТИЧНОГО ВІДБОРУ, ПРОСТОГО ВИПАДКОВОГО ТА СТРАТИФІКОВАНОГО ВІДБОРІВ
2.1 Місто StatVillage
StatVillage – це гіпотетичне місто, яке складається з окремих домогосподарств і використовується як база даних для студентів та аспірантів, що вивчають вибіркові методи.
Дані домогосподарств для StatVillage обирались навмання з результатів перепису сімей, що мешкали в домогосподарствах у місті Ванкувері, Британській Колумбії, Канаді у 1991 році. Сам перепис населення проходив шляхом анонімного анкетування. Бралися до уваги наступн характеристики:
· демографічн показники – розмір домогосподарства та його склад за віком та статтю;
· показники доходу – зайнятість, інвестиції, валові витрати, різні доходи домогосподарств та нші;
· житлов характеристики – тип житла, рік побудови, своє житло чи орендоване, оціночна вартість, щомісячні витрати на розміщення та інші;
· характеристика двох головних членів сім’ї, які відповідають за добробут сім’ї – вік, стать, професія, рідна мова, освіта, зайнятість і т.д;
Існують три конфігурац міста StatVillage:
· Maximal village – складається зі 128 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств - 1024).
· Mini village – складається з 60 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств – 480).
· Micro village – складається з 36 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств – 288).
Кожен блок домогосподарств нумерується в певному порядку, а саме
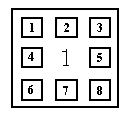
Рис. 2.1.1 Нумерування блоку домогосподарств
Для того, щоб отримати дані з міста StatVillage, необхідно спочатку відмітити домогосподарства позначкою як показано на рисунку 2.1.2 (відмічено кожне 8-ме домогосподарство)

Рис. 2.1.2 Систематично вибірка кожного восьмого домогосподарства
Після цього натискаємо кнопку «Get the sample units» і отримуємо код, який представлений на рис. 2.1.3
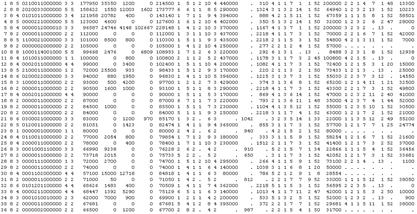
Рис. 2.1.3 Код отримано вибірки
Отриманий код містить 36 стовбців, кожен з яких відповідає за окрему характеристику домогосподарства. Розшифровка коду наведена в додатку А.
2.2 Порівняння відборів
В своїй роботі я використовую другу конфігурацією StatVillage, а саме Mini Village, яка складається з 60-ти блоків. Для того, щоб порівняти точності систематичного, простого випадкового та стратифікованого відборів, я буду використовувати вибірки, добуті з 11-го та 13-го стовпців коду. Ці стовпці називаються TOTINCH та BUILTH, що є загальним доходом домогосподарства (включає в себе заробітну плату, пенсії, дівіденти та відсотки за депозитами і т.д.) та періодом побудови домогосподарства відповідно.
В результаті дослідження виявилось, що домогосподарства в StatVillage впорядковані за загальним доходом, а саме загальний дохід зменшується зі зростанням номеру домогосподарства. Логарифмічна регресія значуща. На рисунку 2.2.1 представлена діаграма розсіювання та логарифмічна регресія.
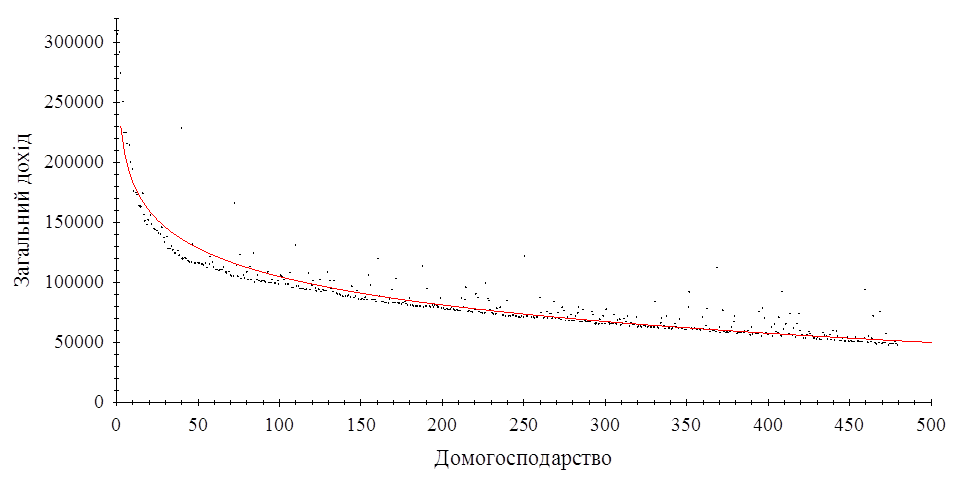 Рис. 2.2.1 Діаграма розсіювання
Рис. 2.2.1 Діаграма розсіювання
Рівняння регресії: ![]() F-статистика:
F-статистика: ![]() Логарифмічна регресія
значуща.
Логарифмічна регресія
значуща.
Порівняємо дисперс середнього доходу домогосподарств при систематичному відборі кожного восьмого домогосподарства, простому випадковому відборі та стратифікованому відборі. Після отримання коду з 11-го стовпця (див. рис 2.1.3) запишемо дані в таблицю 2.2.1, розділивши на 60 страт.
Таблиця 2.2.1 Дані по 8-ми систематичним вибіркам
| Страта | Номер систематичної вибірки (k=8) |
|
|||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 214500 | 306000 | 291178 | 274200 | 250000 | 224230 | 224308 | 215448 | 249983 |
| 2 | 173777 | 200000 | 194322 | 175879 | 175000 | 173058 | 163673 | 162425 | 177266,8 |
| 3 | 143140 | 156667 | 150750 | 148433 | 151774 | 155215 | 147700 | 144781 | 149807,5 |
| 4 | 127600 | 142800 | 140900 | 140000 | 145148 | 137400 | 132998 | 137526 | 138046,5 |
| 5 | 228148 | 127706 | 129400 | 127109 | 124365 | 124324 | 126280 | 122300 | 138704 |
| 6 | 116200 | 120000 | 120393 | 120021 | 117561 | 116876 | 116400 | 131253 | 119838 |
| 7 | 112000 | 116000 | 116000 | 116000 | 115000 | 115400 | 114497 | 115936 | 115104,1 |
| 8 | 110300 | 114766 | 121294 | 117000 | 112100 | 110000 | 110000 | 109600 | 113132,5 |
| 9 | 105000 | 110830 | 112144 | 108481 | 108000 | 108601 | 105493 | 105000 | 107943,6 |
| 10 | 108953 | 165544 | 114427 | 105200 | 122916 | 102865 | 105664 | 102900 | 116058,6 |
| 11 | 100800 | 102400 | 113340 | 101800 | 124400 | 100702 | 102567 | 105400 | 106426,1 |
| 12 | 102400 | 100400 | 101300 | 101000 | 100333 | 108470 | 99070 | 99800 | 101596,6 |
| 13 | 98433 | 99400 | 98957 | 100871 | 98719 | 105833 | 104889 | 101700 | 101100,3 |
| 14 | 96830 | 98100 | 98000 | 107589 | 96050 | 96000 | 130797 | 96193 | 102444,9 |
| 15 | 97700 | 94728 | 94600 | 94542 | 93929 | 93728 | 107275 | 93933 | 96304,38 |
| 16 | 93100 | 100850 | 95029 | 93000 | 93626 | 101800 | 92312 | 93610 | 95415,88 |
| 17 | 90000 | 93082 | 108632 | 101221 | 94304 | 92100 | 101150 | 90800 | 96411,13 |
| 18 | 87000 | 90000 | 88846 | 88697 | 92593 | 88400 | 88000 | 88800 | 89042 |
| 19 | 85500 | 96348 | 87483 | 88615 | 92728 | 86028 | 86000 | 86257 | 88619,88 |
| 20 | 84000 | 87073 | 85320 | 105548 | 97503 | 85800 | 85691 | 85120 | 89506,88 |
| 21 | 85170 | 120000 | 87893 | 83514 | 84134 | 83201 | 83080 | 83000 | 88749 |
| 22 | 82474 | 93489 | 82720 | 82530 | 102614 | 82800 | 82986 | 82080 | 86461,63 |
| 23 | 80000 | 84000 | 81777 | 80539 | 86759 | 81200 | 80800 | 80000 | 81884,38 |
| 24 | 79854 | 80000 | 80400 | 80000 | 113400 | 79350 | 80050 | 94375 | 85928,63 |
| 25 | 78400 | 79000 | 81268 | 79400 | 80800 | 79800 | 79532 | 86117 | 80539,63 |
| 26 | 76228 | 78075 | 77600 | 77985 | 77650 | 77359 | 79122 | 77096 | 77639,38 |
| 27 | 75733 | 77000 | 76149 | 76000 | 86069 | 78974 | 85351 | 95990 | 81408,25 |
| 28 | 74700 | 76400 | 75853 | 75000 | 76983 | 90305 | 87022 | 75528 | 78973,88 |
| 29 | 74000 | 74946 | 74961 | 99015 | 86590 | 84569 | 77300 | 74800 | 80772,63 |
| 30 | 84818 | 73587 | 77909 | 75210 | 79193 | 72400 | 73000 | 72110 | 76028,38 |
| 31 | 71050 | 72093 | 72200 | 72800 | 72800 | 71856 | 72174 | 71238 | 72026,38 |
| 32 | 70509 | 71400 | 71000 | 121762 | 71647 | 71397 | 72458 | 70750 | 77615,38 |
| 33 | 75129 | 70000 | 70800 | 70400 | 87400 | 74915 | 70000 | 70800 | 73680,5 |
| 34 | 69900 | 69731 | 73282 | 73792 | 69470 | 83568 | 69833 | 74300 | 72984,5 |
| 35 | 67681 | 69105 | 79079 | 76779 | 68550 | 71178 | 68033 | 72400 | 71600,63 |
| 36 | 67700 | 68400 | 71570 | 74400 | 78843 | 67400 | 67000 | 77141 | 71556,75 |
| 37 | 65659 | 66703 | 67217 | 66800 | 75000 | 72439 | 65400 | 66132 | 68168,75 |
| 38 | 65000 | 69320 | 65000 | 71800 | 65000 | 76890 | 66154 | 65500 | 68083 |
| 39 | 69600 | 65300 | 73111 | 65065 | 68457 | 69200 | 64400 | 65229 | 67545,25 |
| 40 | 63000 | 67200 | 71943 | 63652 | 66020 | 64400 | 63993 | 70740 | 66368,5 |
| 41 | 62900 | 63800 | 63800 | 62893 | 63200 | 63200 | 62697 | 63306 | 63224,5 |
| 42 | 63519 | 62500 | 62763 | 83643 | 62400 | 62095 | 65900 | 69725 | 66568,13 |
| 43 | 62364 | 61611 | 71443 | 61304 | 61300 | 61200 | 61908 | 65000 | 63266,25 |
| 44 | 92240 | 61400 | 68700 | 61355 | 61623 | 60468 | 61151 | 79534 | 68308,88 |
| 45 | 71233 | 61612 | 60800 | 61800 | 62000 | 60800 | 60910 | 60000 | 62394,38 |
| 46 | 58988 | 60374 | 63684 | 78065 | 60733 | 59000 | 59400 | 59400 | 62455,5 |
| 47 | 58400 | 111951 | 62227 | 58224 | 76761 | 58975 | 58000 | 58450 | 67873,5 |
| 48 | 57800 | 58500 | 62910 | 66981 | 71500 | 57400 | 57600 | 57800 | 61311,38 |
| 49 | 58354 | 57800 | 58871 | 58544 | 60217 | 56358 | 62763 | 57060 | 58745,88 |
| 50 | 55900 | 56800 | 57467 | 75196 | 55479 | 78122 | 69699 | 57527 | 63273,75 |
| 51 | 55350 | 56685 | 62369 | 55000 | 65300 | 59148 | 58400 | 71000 | 60406,5 |
| 52 | 61671 | 91516 | 61052 | 65277 | 56550 | 56850 | 73512 | 56000 | 65303,5 |
| 53 | 56467 | 54000 | 65700 | 73998 | 59781 | 55788 | 53530 | 53000 | 59033 |
| 54 | 52191 | 58700 | 57219 | 55441 | 53533 | 53300 | 52163 | 53879 | 54553,25 |
| 55 | 59391 | 52621 | 58086 | 55800 | 55500 | 52475 | 55818 | 52335 | 55253,25 |
| 56 | 51000 | 51713 | 59277 | 55347 | 51333 | 51600 | 53465 | 51857 | 53199 |
| 57 | 50527 | 54560 | 51000 | 51857 | 50859 | 50800 | 54540 | 50700 | 51855,38 |
| 58 | 53475 | 50500 | 50460 | 53426 | 93669 | 50000 | 55000 | 50800 | 57166,25 |
| 59 | 49517 | 71853 | 49400 | 49000 | 49214 | 75349 | 48594 | 49582 | 55313,63 |
| 60 | 47900 | 57499 | 48000 | 48992 | 48360 | 48400 | 50649 | 49105 | 49863,13 |
|
|
83852,88 | 88407,3 | 86154,58 | 86896,53 | 87045,67 | 83855,98 | 83469,18 | 83002,8 | 5120137 |
|
|
5031173 | 5304438 | 5169275 | 5213792 | 5222740 | 5031359 | 5008151 | 4980168 | |
У кожній страті міститься 1 блок, тобто 8 домогосподарств.
Знайдемо середнє та дисперсію для всієї популяції:
![]()
![]()
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
![]() .
.
Середнє значення систематичної вибірки має розподіл
![]() ~
~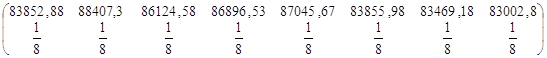
![]()
Оцінка ![]() є незміщеною оцінкою для
є незміщеною оцінкою для ![]() , дійсно
, дійсно ![]() .
.
![]()
Дисперсія систематично вибірки дорівнює
![]()
Тепер знайдемо дисперсію одиниць, що належать до однієї і тієї самої страти:
![]()
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
![]() .
.
Отже, ми отримали такі результати:
![]()
![]()
![]() .
.
Це означає, що
![]() .
.
При наявності логарифмічно залежності між загальним доходом та номером домогосподарства систематичний відбір виявився точнішим за простий випадковий та стратифікований відбори.
Тепер розглянемо дані, в яких відсутній тренд. Використовуємо вибірки, добуті з 13-го стовпця коду. Цей стовбець має назву BUILTH і відповідає за період побудови домогосподарства.
В результаті дослідження даної вибірки, виявилось, що залежність між періодом побудови та номером домогосподарства відсутня. Лінійна регресія не значуща. На рисунку 2.2.2 представлена діаграма розсіювання та відсутність лінійної регресії.
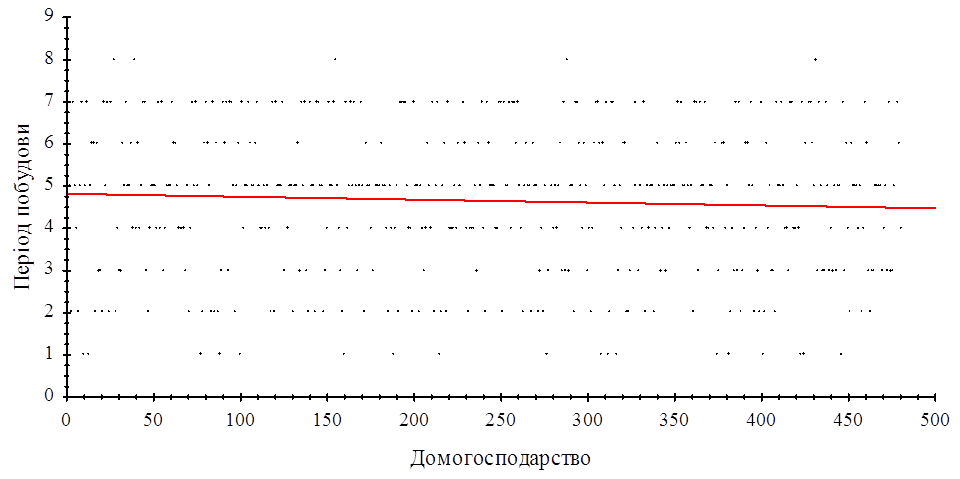 Рис. 2.2.2 Діаграма розсіювання
Рис. 2.2.2 Діаграма розсіювання
Рівняння регресії: ![]() F-статистика:
F-статистика: ![]() Лінійна регресія не
значуща
Лінійна регресія не
значуща
Порівняємо дисперсії середнього періоду побудови домогосподарства при систематичному відборі кожного восьмого домогосподарства, простому випадковому відборі та стратифікованому відборі. Після отримання коду з 13-го стовпця (див. рис 2.1.3) запишемо дані в таблицю 2.2.2, розділивши на 60 страт.
Таблиця 2.2.2 Дані по 8-ми систематичним вибіркам
| Страта | Номер систематичної вибірки (k=8) |
|
|||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 5 | 7 | 5 | 2 | 7 | 5 | 4 | 2 | 4,625 |
| 2 | 6 | 7 | 1 | 5 | 7 | 1 | 5 | 6 | 4,75 |
| 3 | 7 | 2 | 6 | 3 | 3 | 2 | 7 | 5 | 4,375 |
| 4 | 6 | 2 | 7 | 8 | 2 | 4 | 3 | 3 | 4,375 |
| 5 | 4 | 5 | 7 | 5 | 5 | 6 | 4 | 8 | 5,5 |
| 6 | 4 | 6 | 4 | 5 | 7 | 7 | 3 | 2 | 4,75 |
| 7 | 3 | 5 | 5 | 5 | 4 | 7 | 4 | 7 | 5 |
| 8 | 5 | 4 | 5 | 5 | 5 | 7 | 6 | 6 | 5,375 |
| 9 | 4 | 4 | 4 | 4 | 4 | 3 | 5 | 2 | 3,75 |
| 10 | 7 | 7 | 5 | 7 | 5 | 1 | 2 | 6 | 5 |
| 11 | 1 | 6 | 5 | 2 | 7 | 2 | 6 | 2 | 3,875 |
| 12 | 5 | 3 | 7 | 6 | 7 | 3 | 7 | 7 | 5,625 |
| 13 | 5 | 2 | 5 | 6 | 1 | 7 | 4 | 5 | 4,375 |
| 14 | 4 | 7 | 6 | 5 | 5 | 6 | 7 | 5 | 5,625 |
| 15 | 2 | 4 | 5 | 4 | 5 | 4 | 2 | 7 | 4,125 |
| 16 | 5 | 7 | 5 | 5 | 5 | 7 | 3 | 4 | 5,125 |
| 17 | 5 | 5 | 2 | 5 | 5 | 6 | 3 | 7 | 4,75 |
| 18 | 7 | 7 | 3 | 2 | 7 | 5 | 5 | 2 | 4,75 |
| 19 | 5 | 7 | 5 | 5 | 2 | 3 | 4 | 7 | 4,75 |
| 20 | 1 | 5 | 7 | 8 | 5 | 4 | 3 | 2 | 4,375 |
| 21 | 3 | 7 | 4 | 5 | 7 | 5 | 7 | 5 | 5,375 |
| 22 | 4 | 5 | 7 | 5 | 2 | 6 | 5 | 5 | 4,875 |
| 23 | 4 | 3 | 5 | 5 | 5 | 6 | 5 | 5 | 4,75 |
| 24 | 7 | 2 | 5 | 4 | 1 | 4 | 5 | 2 | 3,75 |
| 25 | 7 | 7 | 7 | 7 | 5 | 4 | 4 | 2 | 5,375 |
| 26 | 6 | 5 | 5 | 2 | 5 | 4 | 3 | 4 | 4,25 |
| 27 | 2 | 5 | 4 | 7 | 2 | 5 | 7 | 1 | 4,125 |
| 28 | 5 | 5 | 6 | 2 | 7 | 4 | 4 | 4 | 4,625 |
| 29 | 4 | 4 | 6 | 5 | 7 | 6 | 4 | 2 | 4,75 |
| 30 | 4 | 4 | 4 | 5 | 3 | 6 | 5 | 7 | 4,75 |
| 31 | 4 | 2 | 7 | 6 | 5 | 5 | 5 | 4 | 4,75 |
| 32 | 4 | 7 | 7 | 2 | 7 | 5 | 5 | 7 | 5,5 |
| 33 | 5 | 7 | 7 | 6 | 7 | 5 | 4 | 2 | 5,375 |
| 34 | 2 | 6 | 5 | 5 | 2 | 6 | 5 | 5 | 4,5 |
| 35 | 4 | 3 | 4 | 2 | 5 | 1 | 3 | 5 | 3,375 |
| 36 | 8 | 5 | 4 | 5 | 6 | 3 | 7 | 3 | 5,125 |
| 37 | 5 | 3 | 5 | 5 | 2 | 7 | 7 | 6 | 5 |
| 38 | 6 | 4 | 6 | 5 | 3 | 4 | 2 | 4 | 4,25 |
| 39 | 1 | 7 | 7 | 6 | 1 | 6 | 5 | 7 | 5 |
| 40 | 4 | 2 | 7 | 7 | 5 | 1 | 3 | 5 | 4,25 |
| 41 | 7 | 6 | 6 | 2 | 2 | 3 | 4 | 5 | 4,375 |
| 42 | 5 | 3 | 5 | 4 | 7 | 2 | 5 | 4 | 4,375 |
| 43 | 5 | 5 | 2 | 4 | 6 | 5 | 3 | 4 | 4,25 |
| 44 | 7 | 3 | 5 | 4 | 5 | 5 | 5 | 6 | 5 |
| 45 | 5 | 6 | 7 | 5 | 5 | 6 | 5 | 4 | 5,375 |
| 46 | 7 | 2 | 7 | 7 | 3 | 7 | 5 | 5 | 5,375 |
| 47 | 3 | 4 | 4 | 5 | 5 | 4 | 6 | 1 | 4 |
| 48 | 3 | 6 | 6 | 4 | 5 | 1 | 2 | 4 | 3,875 |
| 49 | 6 | 7 | 3 | 7 | 2 | 3 | 4 | 6 | 4,75 |
| 50 | 7 | 5 | 7 | 5 | 2 | 4 | 3 | 2 | 4,375 |
| 51 | 2 | 1 | 2 | 6 | 4 | 5 | 3 | 3 | 3,25 |
| 52 | 3 | 7 | 5 | 5 | 7 | 5 | 4 | 4 | 5 |
| 53 | 7 | 7 | 7 | 4 | 4 | 5 | 4 | 1 | 4,875 |
| 54 | 3 | 1 | 6 | 7 | 7 | 6 | 5 | 8 | 5,375 |
| 55 | 4 | 7 | 5 | 3 | 3 | 7 | 5 | 3 | 4,625 |
| 56 | 3 | 3 | 5 | 3 | 5 | 5 | 1 | 7 | 4 |
| 57 | 4 | 6 | 4 | 2 | 6 | 5 | 5 | 5 | 4,625 |
| 58 | 3 | 5 | 2 | 4 | 7 | 6 | 3 | 2 | 4 |
| 59 | 5 | 3 | 5 | 5 | 5 | 5 | 3 | 4 | 4,375 |
| 60 | 4 | 3 | 7 | 3 | 3 | 5 | 7 | 6 | 4,75 |
|
|
4,55 | 4,75 | 5,18 | 4,7 | 4,63 | 4,62 | 4,4 | 4,4 | 279,25 |
|
|
273 | 285 | 311 | 282 | 278 | 277 | 264 | 264 | |
Знайдемо середнє та дисперсію для всієї популяції:
![]()
![]()
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
![]() .
.
Середнє значення систематично вибірки має розподіл
![]() ~
~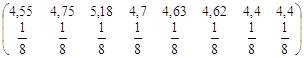
![]()
Також отримали, що ![]() .
.
![]()
Дисперсія систематично вибірки дорівнює
![]()
Тепер знайдемо дисперсію одиниць, що належать до однієї і тієї самої страти:
![]()
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
![]() .
.
Отже, ми отримали так результати:
![]()
![]()
![]() .
.
Це означає, що
![]() .
.
При відсутності тренду систематичний відбір виявився ефективнішим ніж стратифікований відбір, але менш точним ніж простий випадковий відбір. Якщо порівняти дисперсії систематичної та простої випадкової вибірок, то виявиться що вони дуже мало відрізняються. При випадковому порядку розміщення одиниць систематичний відбір в середньому рівносильний простому випадковому відбору (останнє підтверджує теоретичні положення підрозділу 1.3).
Для підвищення точност систематичного відбору, при дослідженні періоду побудови домогосподарства, застосуємо стратифікований систематичний відбір. Основна його ідея розглядалась у підрозділі 1.9. Отже, всю популяцію, яка складається з 60-ти блоків (по 8 домогосподарств у кожному), ділимо на 2 страти. В першій страті розміщуються з 1-го по 32-й блоки (тобто 256 домогосподарств), а в другій – з 33-го по 60-й блоки (224 домогосподарства). З кожної страти здобуваємо систематичні вибірки кожно 8-ї одиниці. Всього комбінацій здобуття таких систематичних вибірок з двох страт – 64 (8 комбінацій з першої страти та 8 – з другої страти). Середн значення стратифікованої систематичної вибірки рахується за формулою
![]() ,
,
де ![]() - це вага страти
- це вага страти ![]() , а
, а ![]() - середнє значення
систематичної вибірки у страті
- середнє значення
систематичної вибірки у страті ![]() .
.
Так як я буду розглядати 2 страти, то середнє значення стратифікованої систематичної вибірки має вигляд:
![]()
![]()
![]()
а ![]() для
кожної систематичної вибірки у першій або другій страті своє.
для
кожної систематичної вибірки у першій або другій страті своє.
Після розглядання всіх
стратифікованих систематичних вибірок кожної 8-ї одиниці запишемо розподіл ![]() :
:
![]()
![]()
![]()
Також має місце рівність ![]() .
.
![]()
Дисперсія середнього стратифікованої систематичної вибірки дорівнює:
![]() .
.
При застосуванн стратифікованого систематичного відбору для періоду побудови домогосподарства маємо наступні результати:
![]()
![]()
![]() .
.
Це означає, що
![]() .
.
При відсутності тренду стратифікований систематичний відбір є точнішим за простий випадковий та стратифікований відбори. Тобто стратифікований систематичний відбір дає більш точну оцінку ніж звичайний систематичний відбір.
Висновки
Вибірковий метод – метод дослідження, що дозволяє робити висновок про характер розподілу досліджуваних ознак популяції на основі розгляду деякої її частини (тобто вибірки). Прикладом вибіркових обстежень може бути визначення середнього рівня доходів населення, визначення переліку споживчих переваг, визначення рейтингу кандидата на виборах та інші. Існують різні методи вибіркового обстеження: простий випадковий відбір, стратифікований відбір, систематичний відбір, кластерний та інші. Для різних популяцій різні методи відбору можуть бути більш точними або менш точними.
Розглянемо простий,
систематичний та стратифікований відбори. Простим випадковим відбором
називається спосіб добування ![]() одиниць
вибірки з
одиниць
вибірки з ![]() одиниць популяції так, що
кожна з
одиниць популяції так, що
кожна з ![]() вибірок має рівну
мовірність бути відібраною. За допомогою таблиці або датчика випадкових чисел
добуваємо вибірку обсягом
вибірок має рівну
мовірність бути відібраною. За допомогою таблиці або датчика випадкових чисел
добуваємо вибірку обсягом ![]() .
.
Систематичний відбір поляга
у тому, що з популяції, одиниці якої перенумеровані від 1 до ![]() , для здобуття вибірки
обсягу
, для здобуття вибірки
обсягу ![]() спочатку навмання
вибираємо будь-яку одиницю з перших
спочатку навмання
вибираємо будь-яку одиницю з перших ![]() одиниць
популяції (наприклад, п’яту одиницю з 8-ми одиниць). Після вибору першо
одиниці вибираємо кожну
одиниць
популяції (наприклад, п’яту одиницю з 8-ми одиниць). Після вибору першо
одиниці вибираємо кожну ![]() -ту
одиницю популяції (тобто 10-ту, 15-ту, 20-ту, 25-ту,….,
-ту
одиницю популяції (тобто 10-ту, 15-ту, 20-ту, 25-ту,….,![]() -ту). Таку вибірку
називають систематичною вибіркою кожної
-ту). Таку вибірку
називають систематичною вибіркою кожної ![]() -
одиниці.
-
одиниці.
Стратифікований відбір
полягає в тому, що вся популяція поділяється на менші під популяції (страти),
які не мають спільних одиниць і кожна з яких внутрішньо однорідна. Потім за
допомогою простого випадкового відбору з кожної страти здобувається вибірка.
Такий відбір називається стратифікованим випадковим відбором. Наприклад,
популяція з ![]() одиниць поділена на
одиниць поділена на ![]() страт, по 8 одиниць у
кожній страті. З кожної страти здобуваємо по 2 одиниці за допомогою таблиці або
датчика випадкових чисел. В результаті отримаємо: в першій страті числа 2, 7; в
другій страті - 13, 16; і т.д.
страт, по 8 одиниць у
кожній страті. З кожної страти здобуваємо по 2 одиниці за допомогою таблиці або
датчика випадкових чисел. В результаті отримаємо: в першій страті числа 2, 7; в
другій страті - 13, 16; і т.д.
В роботі ставиться задача порівняння точності систематичного відбору, простого випадкового та стратифікованого відбору.
Для розв’язання цієї задач використано наступні теоретичні положення.
1. Середнє значення ![]() систематичної вибірки
незміщеною оцінкою для середнього значення популяції
систематичної вибірки
незміщеною оцінкою для середнього значення популяції ![]() .
.
![]() (1)
(1)
2. Дисперсія середнього значення систематичної вибірки визначається формулою (2)
![]() (2)
(2)
де дисперсія одиниць, як належать одній систематичній вибірці визначається формулою (3),
![]() (3)
(3)
а дисперсія популяц визначається формулою (4)
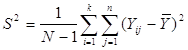 (4)
(4)
3. Середнє значення для систематично вибірки більш точне, ніж середнє для простої випадкової вибірки
![]()
тоді і тільки тоді, коли справедлива нерівність (5)
![]() . (5)
. (5)
4. Дисперсія середнього значення систематичної вибірки може визначатись й формулою (6)
![]() , (6)
, (6)
де ![]() - коефіцієнт кореляц
між парами одиниць, що належать до однієї й тієї самої систематичної вибірки.
- коефіцієнт кореляц
між парами одиниць, що належать до однієї й тієї самої систематичної вибірки.
![]() (7)
(7)
5. Дисперсія середнього значення систематичної вибірки може ще визначатись формулою (8)
![]() , (8)
, (8)
де дисперсія одиниць, що належать до однієї й тієї самої страти визначається формулою (9)
![]() . (9)
. (9)
Величина
![]() . (10)
. (10)
є коефіцієнтом кореляції між відхиленнями від середнього значення для страти по всім парам одиниць, що належать до однієї й тієї ж систематичної вибірки.
Зауважимо, що формули 2, 6, 8 - еквівалентні
6. Якщо в популяції одиниці розташован
навмання розглянемо всі ![]() скінчених
популяцій, що утворюються за допомогою
скінчених
популяцій, що утворюються за допомогою ![]() перестановок
деякого набору чисел
перестановок
деякого набору чисел ![]() . Тоді в
середньому по всім цим скінченим популяціям справедлива формула (11)
. Тоді в
середньому по всім цим скінченим популяціям справедлива формула (11)
![]() . (11)
. (11)
Тобто, коли одиниці вибірки розташовані випадково систематичний відбір в середньому рівносильний простому випадковому відбору.
Якщо між деякими характеристиками популяції наявна лінійна залежність, то справедлива нерівність (12).
![]() . (12)
. (12)
Тобто, стратифікований відбір точніший за систематичний відбір, який в свою чергу точніший простого випадкового відбору.
В своїй роботі я порівнювала точність систематичного відбору, простого випадкового та стратифікованого відбору, користуючись програмою StatVillage.
StatVillage – це гіпотетичне місто, яке складається з окремих домогосподарств і використовується як база даних для студентів та аспірантів, що вивчають вибіркові методи.
Дані домогосподарств для StatVillage обирались навмання з результатів перепису сімей, що мешкали у міст Ванкувері, Британській Колумбії, Канаді у 1991 році. Сам перепис населення проходив шляхом анонімного анкетування. Бралися до уваги наступн характеристики:
· демографічн показники (розмір домогосподарства та його склад за віком та статтю);
· показники доходу (зайнятість, інвестиції, валові витрати, різні доходи домогосподарств та нші);
· житлов характеристики (тип житла, рік побудови, своє житло чи орендоване, оціночна вартість, щомісячні витрати на розміщення та інші);
· характеристика двох членів сім’ї, які відповідають за добробут сім’ї (вік, стать, професія, рідна мова, освіта, зайнятість і т.д;)
Домогосподарства були розташовані згідно з загальним доходом від найбільшого до найменшого.
Існують три конфігурац міста StatVillage: Maximal village – складається зі 128 блоків, Mini village складається з 60 блоків, та Micro village – складається з 36 блоків.
Для того, щоб отримати дані з міста StatVillage, необхідно спочатку відмітити домогосподарства позначкою. Після чого натискаючи кнопку «Get the sample units», отримуємо код. Отриманий код містить стовпці, кожен з яких відповідає за окрему характеристику домогосподарства
Порівнювати точност систематичного, простого та стратифікованого відборів, я буду використовувати вибірки, добуті з 11 та 13 стовпців коду. Ці стовпці відповідають – загальним доходам домогосподарства (включають в себе заробітну плату, пенсії, дівіденти та відсотки за депозитами) та періоду побудови домогосподарства.
В результаті дослідження виявилося, що загальний дохід зменшується зі зростанням номеру домогосподарства. Логарифмічна регресія значуща. Для загального доходу систематичний відбір виявився точнішим за простий випадковий та стратифікований відбори.
При дослідженні періоду побудови домогосподарства виявилося, що будь-яка залежність відсутня. Лінійна регресія не значуща. Систематичний відбір виявився більш точним ніж стратифікований випадковий відбір, але менш точним у порівнянні з простим випадковим відбором. Але можна помітити, що дисперсії простої випадкової та систематичної відбірок відрізняються мало. Отже, коли одиниці вибірки розташовані випадково систематичний відбір майже рівносильний простому випадковому відбору.
Останню оцінку можна покращити, застосувавши стратифікований систематичний відбір. Для цього всю популяцію ділимо на 2 страти. З кожної страти здобуваємо систематичні вибірки. Всього комбінацій здобуття вибірок з обох страт – 64. Дисперсія середнього стратифікованої систематичної вибірки виявилась меншою за відповідну дисперсію звичайної систематичної вибірки. Отже стратифікований систематичний відбір точнішим за простий випадковий та стратифікований відбори.
Ефективність систематичного відбору в порівнянні зі стратифікованим або простим випадковим відбором суттєво залежить від особливостей популяції. Існують такі популяції, в яких систематичний відбір дає високу точність, але є й такі, для яких простий випадковий відбір є більш точним ніж систематичний. В будь-якому випадку для того, щоб застосування систематичного відбору було ефективним, необхідно знати будову популяції, з якої проводиться відбір.
Систематичні вибірки зручно намічати та вилучати. У більшост
досліджень як по штучним, так і по реальним популяціям, вони вигравали в
точності у порівнянні зі стратифікованими випадковими вибірками. Недоліки систематично
вибірки полягають в тому, що її точність може виявитись невисокою, якщо існу
несподівана періодичність, і в тому, що невідомий надійний метод оцінювання ![]() за даними вибірки. Але не
дивлячись на це, систематичний відбір рекомендований у наступних ситуаціях.
за даними вибірки. Але не
дивлячись на це, систематичний відбір рекомендований у наступних ситуаціях.
1. Якщо одиниці популяції розташовані в основному навмання або якщо стратифікування в популяції намічено досить слабо. В цьому випадку систематичний відбір застосовується, оскільки він зручний і не можна розраховувати на виграш в точності. Є вибіркові оцінки похибки, зміщення яких знаходиться у допустимих границях.
2. Якщо застосовується стратифікування з великим числом страт і систематична вибірка вилучається незалежно з кожній страти. В цьому випадку вплив приховано періодичності має тенденцію нейтралізуватися і можна одержати оцінку похибки, яка заздалегідь перевищена. При іншому способі можна скористатися лише половиною страт та вилучити з кожної страти по дві систематичні вибірки з незалежним випадковим початком відліку. Такий спосіб забезпечує незміщену оцінку похибки.
3. При підвідборі одиниць. В цьому випадку виявляється, що у більшості практичних додатків можна отримати незміщену оцінку похибки вибірки.
4. При вибірковому вивчені популяцій з варіацією неперервного характеру за умови, що оцінка похибки вибірки звичайно не вимагається. Якщо проводиться ряд обстежень такого типу, то може виявитись достатнім перевіряти похибки вибірки лише від випадку до випадку. Йейтс (1948) вказує, що можна робити таку перевірку за допомогою додаткових спостережень.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Кокрен У. Методы выборочного исследования. Пер. с англ. И.М. Сонина. Под ред. А.Г. Волкова. – М.: Статистика, 1976. – 440 с. с ил.
2. Черняк О.І. Техніка вибіркових досліджень. – К.: МІВВЦ, 2001. – 248 с.
3. Пархоменко В.М. Методи вибіркових обстежень. Навчальний посібник. – К.,2001. – 148 с.
4. Govindarajulu Z. “Elements of sampling theory and methods”
5. Sharon L. Lohr Sampling: Design and Analysis – Duxbury Press, 1999. – 253c.